Contetns
- Spanning Tree
- Minimum Spanning Tree
- Prim Algorithm
- MSTNode
- MSTEdge
- MSTGraph
- Test
- Reference
Spanning Tree(스패닝 트리)
그래프 G의 스패닝 트리(Spnning Tree) T는 일종의 서브그래프로서, G의 모든 꼭지점을 포함하는 트리다. 이 조건을 충족하기 위해 G는 반드시 모든 노드가 서로 연결돼 있어야 합니다(즉, 모든 꼭지점은 다른 꼭지점과 적어도 한 번 이상 연결돼야 합니다)
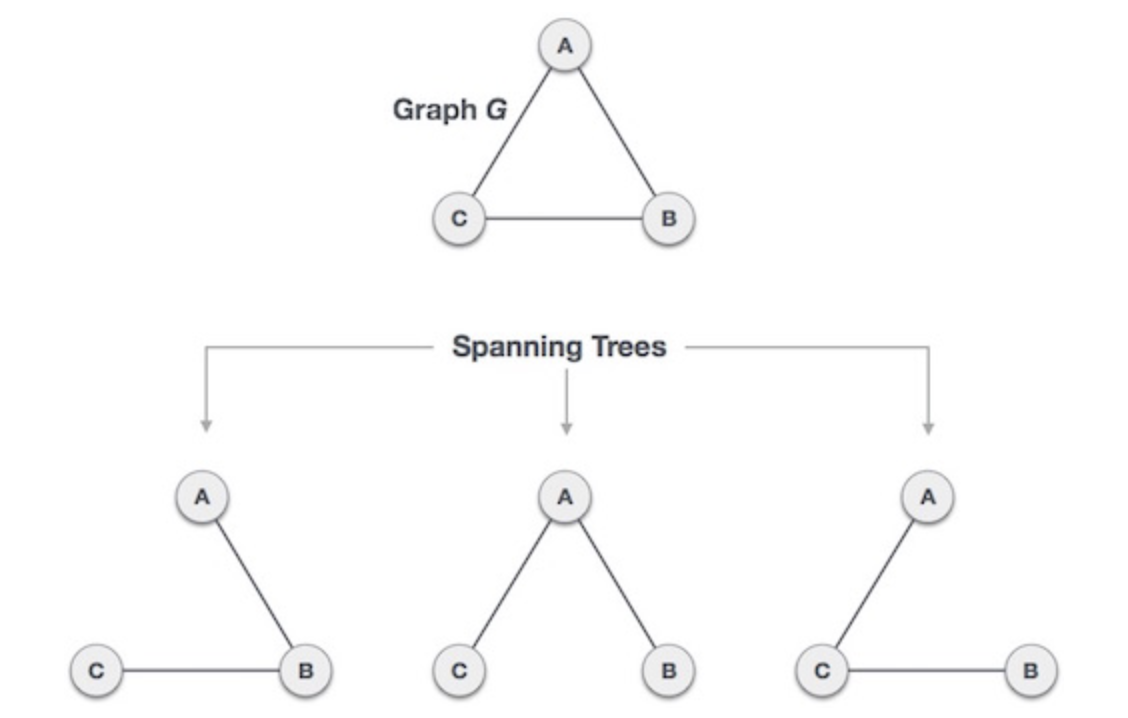
위 그림에서 알 수 있듯, 하나의 그래프 G에서는 하나 이상의 다양한 스패닝 트리가 나탈 수 있습니다. 그래프 G가 트리라면 오직 하나의 스패닝 트리를 지닐 수 있으며, 자기 자신의 모습이 스패닝 트리가 됩니다.
그래프 스패닝 트리
A A
⎮ ⎮
B B
⎮ ⎮
⎮ \ ⎮ \
C D C D
스패닝 트리 애플리케이션은 경로 찾기 알고리즘(다이크스트라), 음성인식, 순환을 피하기 위한 인터넷 라우팅 프로토콜 기술 등 다양한 방면에서 활용되고 있다. 이들 대부분은 어떤 형태로든 스패닝 트리를 사용하고 있으며, 다음 절에서 상세히 알아봅니다.
Minimum Spanning Tree
우리가 어떤 문제를 해결하기 위해 그래프를 사용할 때, 꼭지점과 모서리 이외의 추가적인 정보를 처리해야 할 경우가 있습니다. 각각의 모서리는 비용, 가중치, 특정 유형의 길이 등을 나타낼 수 있는 것입니다. 이런 경우, 모든 꼭지점을 순회한 뒤 도달하기 위한 최소 비용이라는 개념으로 접근해야 할 경우가 있습니다.
디음과 같은 미니멈 스패닝 트리(MST 사례를 살펴봅니다. 각각의 모서리에 가중치 가 있는 무 방향성 그래프 G에서 여러 유형의 스패닝 트리가 만들어 질 수 있는데, MST는 그 중 전체 가중치가 가장 작은 스패닝 트리를 의미합니다(이때 전체 가중치는 모든 모서리의 가중치의 합계가 됩니다.)
MST는 실제 생활에서는 어떻게 활용될까? 경로 찾기의 가장 일반적인 문제는 A에서 D로 이동하면서 B와 C를 경유할 때 최소 이동 시간을 파악하는 것이며, 이것이 바로 MST의 구현 이유입니다.
MST는 그래프에 포함된 모든 꼭지점 사이를 이동할 수 있는 최소 비용의 경로를 알려 줍니다.
Prim Algorithm
Prim 알고리즘은 1957년, 벨 연구소의 수학자이자 컴퓨터 과학자인 로버트 프림이 창안한 것으로, 양방향 연결 그래프를 이용해서 선형 시간내에 MST를 계산하기 위해 만들어 졌습니다.
MST의 계산 절차는 다음과 같습니다
A ㅡ3ㅡ B ㅡ2ㅡ D
\ ⎮
1 1
\ ⎮
C
- 그래프에서 임의의 곡지점을 출발 위치로 선택합니다. 이번 예제에서는 편의상 꼭지점 A에서 출발합니다. 꼭지점 A가 트리의 초기 위치가 됩니다
- 선택된 노드에 연결된 모서리에서 아직 방문하지 않았고, 가중치가 최소인 것을 선택합니다. 이번 예제에서는 A에서 C로 이동하고, C에 방문 표식을 남긴 뒤 MST속에 해당 모서리 정보를 저장합니다.
- 가장 최근 방문 표식이 있는 노드에서 출발합니다. 이번 예제에서는 C가 됩니다. 이 와같은 절차를 그래프의 모든 꼭지점을 대상으로 시행 합니다.
MSTNode
public class DijkstraNode<T: Equatable & Hashable>: Equatable {
// 값, 방문상태, 참조값 변수
public var value: T
public var edges: [DijkstraEdge<T>]
public var visited: Bool
// 출발지점에서 현재 노드에 이르는 최단 거리
public var distance: Int = Int.max
// 최단 경로에 이르는 기존의 노드
// 각 노드에 이르는 경로를 각 노드의 최단 경로로 저장해야 하기 위한 변수
public var previous: DijkstraNode<T>?
public init(value: T, edges: [DijkstraEdge<T>], visited: Bool) {
self.value = value
self.edges = edges
self.visited = visited
}
public static func == <T: Equatable> (lhs: DijkstraNode<T>, rhs: DijkstraNode<T>) -> Bool {
guard lhs.value == rhs.value else { return false }
return true
}
}
extension DijkstraNode: Hashable {
public var hashValue: Int {
get {
return value.hashValue
}
}
}
모서리 배열, 그리고 특정 노드의 방문 여부를 표시하기 위한 불리언 값에 대한 변수가 포함돼 있습니다.
MSTEdge
import Foundation
public class DijkstraEdge<T: Equatable & Hashable>: Equatable {
public var from: DijkstraNode<T>
public var to: DijkstraNode<T>
public var weight: Double
public init(weight: Double, from: DijkstraNode<T>, to: DijkstraNode<T>) {
self.weight = weight
self.from = from
self.to = to
from.edges.append(self)
}
public static func == <T: Equatable> (lhs: DijkstraEdge<T>, rhs: DijkstraEdge<T>) -> Bool {
guard lhs.from.value == rhs.from.value else { return false }
guard lhs.to.value == rhs.from.value else { return false }
return true
}
}
extension DijkstraEdge: Hashable {
public var hashValue: Int {
let stringHash = "\(from.value)->\(to.value)"
return stringHash.hashValue
}
}
위 코드를 통해 그래프의 모서리, 모서리에 연결된 두 개 노드의 참조값, 그리고 모서리의 가중치를 저장하기 위한 제네릭값 등을 만들었습니다.
이제 그래프를 구현하기 위한 클래스를 생성합니다.
MSTGraph
public class DijkstraGraph<T: Equatable & Hashable> {
public var nodes: [DijkstraNode<T>]
public init(nodes: [DijkstraNode<T>]) {
self.nodes = nodes
}
}
위 코드를 통해 꼭지점과 모서리를 저장하고 구현을 마치는 즉시 MST를 출력할수 있는 메소드를 호출할 수 있는 Graph 클래스를 생성합니다.
let nodeA = MSTNode(value: "A", edges: [], visited: false)
let nodeB = MSTNode(value: "B", edges: [], visited: false)
let nodeC = MSTNode(value: "C", edges: [], visited: false)
let nodeD = MSTNode(value: "D", edges: [], visited: false)
let edgeAB = MSTEdge(weight: 3, from: nodeA, to: nodeB)
let edgeBA = MSTEdge(weight: 3, from: nodeB, to: nodeA)
let edgeAC = MSTEdge(weight: 1, from: nodeA, to: nodeC)
let edgeCA = MSTEdge(weight: 1, from: nodeC, to: nodeA)
let edgeBC = MSTEdge(weight: 1, from: nodeB, to: nodeC)
let edgeCB = MSTEdge(weight: 1, from: nodeC, to: nodeB)
let edgeBD = MSTEdge(weight: 2, from: nodeB, to: nodeD)
let edgeDB = MSTEdge(weight: 2, from: nodeD, to: nodeB)
let graph = MSTGraph(nodes: [nodeA, nodeB, nodeC, nodeD])
print(graph)
이제 Prim 알고리즘을 구현해봅니다. MSTGraph.swift 클래스에 다음 메소드를 추가합니다.
public static func minimumSpanningTree(startNode: MSTNode<T>, graph: MSTGraph<T>) {
// 모서리 값을 처리하고 (아직은 방문하지 않은 노드의 최솟값을 선택하기 위해 방문 노드 관리용 배열을 사용합니다
var visitedNodes: [MSTNode<T>] = []
// 첫번째 노드를 출력하고, 모서리 값을 처리하기 위해 visitedNodes배열에 추가합니다.
print(startNode.value)
visitedNodes.append(startNode)
startNode.visited = true
// 그래프의 모든 노드를 방문할 때 까지 반복합니다.
while visitedNodes.count < graph.nodes.count {
// 가장 먼저 무한 반복을 피하기 위해 아직 방문하지 않은 모든 모서리를 추출 합니다
var unvisitedEdges: [MSTEdge<T>] = []
_ = visitedNodes.map{ (node) -> () in
let edges = node.edges.filter{ (edge) -> Bool in edge.to.visited == false }
// 방문하지 않은 모서리를 필터한후, 해당 모서리들 방문하지 않은 모서리에 업데이트
unvisitedEdges.append(contentsOf: edges)
}
/*
모서리 배열에서 가중치가 좀더 작은 것을 선택 및
출력하고 while 루프의 다음 순회 시에도 노드를 계속
처리할 수 있도록 visitedNode 배열에 추가합니다.
*/
if let minimumUnvisitedEdge = unvisitedEdges.sorted(by: { (edgeA, edgeB) -> Bool in
edgeA.weight < edgeB.weight}).first {
print("\(minimumUnvisitedEdge.from.value) <--------> \(minimumUnvisitedEdge.to.value)")
minimumUnvisitedEdge.to.visited = true
visitedNodes.append(minimumUnvisitedEdge.to)
}
}
}
이제 미니멈 스패닝 트리를 위한 메소드 또한 만들었습니다.
Test
MSTGraph.minimumSpanningTree(startNode: nodeA, graph: graph)
위 출력 결과를 보면 이번 그래프의 MST는 A->C->B->D 임을 알 수 있다. 잠시 후 이번 결과와 비교할 수 있는 또 다른 사례를 살펴볼 것입니다.
출력결과
A <--------> C
C <--------> B
B <--------> D
이번에는 B <-> C 구간의 가중치를 100으로 변경하여 다시 출력해보자.
출력결과
A <--------> C
A <--------> B
B <--------> D
Reference
Data Structures and Algorithms in Swift
swift-algorithm-club/Minimum Spanning Tree (Unweighted)
swift-algorithm-club/Minimum Spanning Tree