Contetns
- Dijkstra Alogrithm
- Example
- First pass
- Second pass
- Third pass
- Fourth pass
- Fifth pass
- Sixth pass
- Seventh pass
- Eighth pass
- Implementation
- Dijkstra Node
- Dijkstra Edge
- DijkstraGraph
- Reference
Dijkstra Alogrithm
Google 또는 Apple지도 앱을 사용하여 한 곳에서 다른 곳으로 가장 짧은 또는 가장 빠른 것을 찾았습니까? Dijkstra의 알고리즘은 GPS 네트워크에서 두 곳 사이의 최단 경로를 찾는 데 특히 유용합니다.
Dijkstra의 알고리즘은 욕심 많은 알고리즘입니다. 욕심 많은 알고리즘은 단계별로 솔루션을 구성하고 모든 단계에서 최적의 경로를 선택합니다. 특히, Dijkstra의 알고리즘은 방향이 정해진 그래프와 방향이 없는 그래프에서 꼭지점 간 최단 경로를 찾습니다. 그래프의 꼭지점이 주어지면 알고리즘은 시작점에서부터 가장 짧은 경로를 모두 찾습니다.
다익스트라 알고리즘의 사용되어지는 예들입니다
- 전염성 질병 전파: 생물학적 질병이 가장 빠르게 퍼지고 있는 곳을 찾으세요
- 전화 네트워크: 네트워크에서 사용할 수 있는 최고 대역폭 경로로 호출을 라우팅 합니다
- 지도: 가장 짧고 빠른 경로를 찾는 것이 여행하는 모든 사람들에게 중요합니다
Example
아래의 그래프는 GPS 네트워크를 나타냅니다. 꼭지점은 물리적 위치를 나타내며 꼭지점 사이의 모서리는 위치 사이의 주어진 비용의 편도 경로를 나타냅니다.
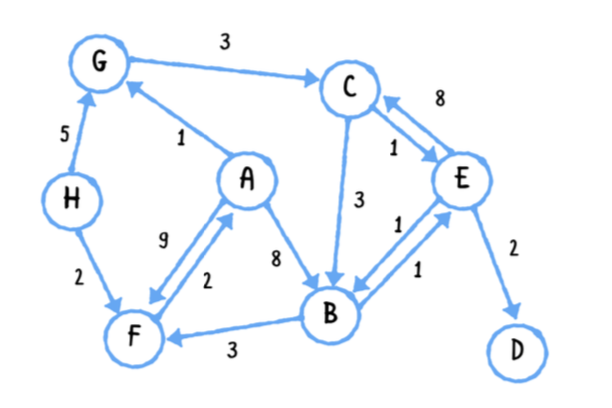
다익스트라 알고리즘에서 첫번째로 시작꼭지점이 필요하기 떄문에 시작 꼭지점을 선택합니다. 선택된 시작 꼭지점을 꼭지점 A 라고 가정합니다.
First pass
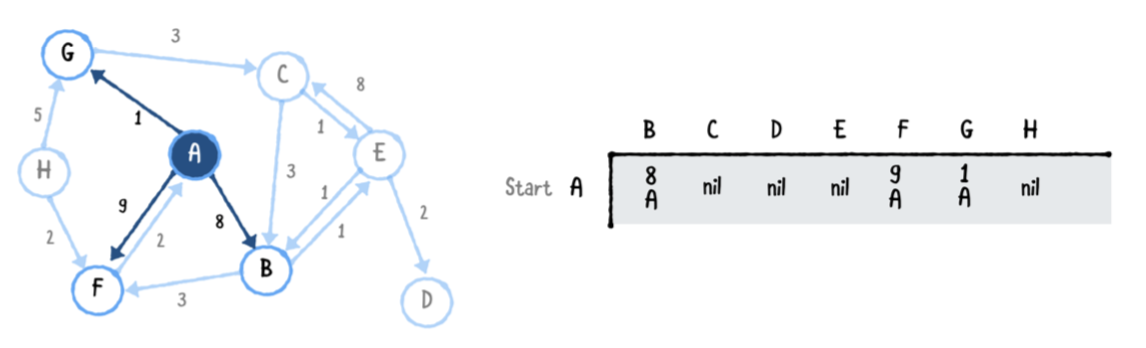
꼭지점 A로 부터 모든 모서리를 바라봅니다. 이 경우에 세개의 모서리가 있습니다
- A -> B, 8의 가중치를 가지고 있습니다.
- A -> F, 9의 가중치를 가지고 있습니다.
- A -> G, 1의 가중치를 가지고 있습니다.
나머지 꼭지점들은(The remainder of the vertices)는 nil로 표시하고, 거기는 A에서 직접적으로 갈수 없습니다.
이 예제를 진행하면서, 그래프의 오른쪽 테이블은 각 스테이지에서 다익스트라 알고리즘의 자취를 표현하고, 기록합니다.
알고리즘의 각 패스는 테이블에 행에 추가합니다. 테이블의 마지막 행은 알고리즘의 최종 출력이 됩니다.
Second pass
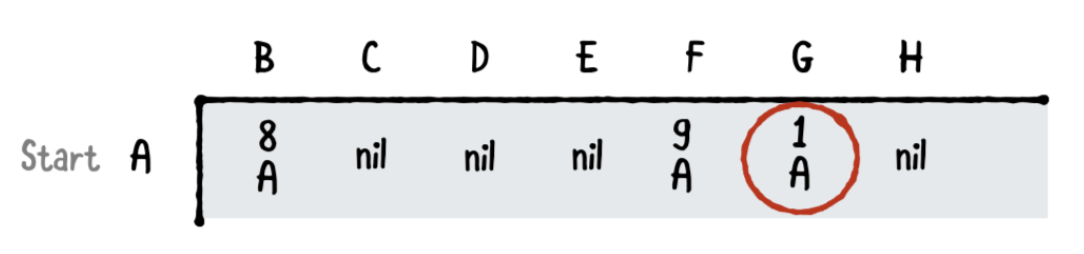
다음 싸이클에서, 다익스트라의 알고리즘은 지금까지 가지고 있던 길들 중 가장낮은 값의 경로를 봅니다. A에서 G로 가는것은 비용1로 가장 적은 비용을 가지고, A에서 G로 가는 가장 짧은 길이기도 합니다. 이것은 출력 테이블에 어둡게 채워져서 표시됩니다.
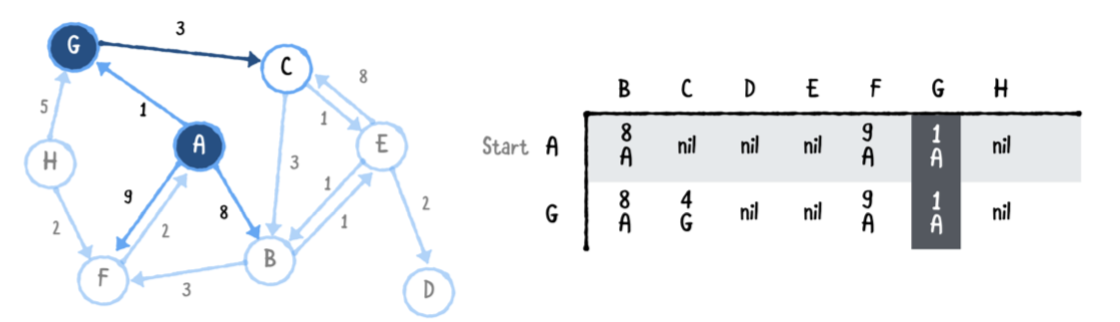
이제 최저 비용 경로 인 꼭지점 G에서 모든 모서리를 살펴봅니다. G에서 C까지 단 하나의 모서리 만 있고 총 비용은 4입니다. 이는 A에서 G까지의 비용이 1 + 3 = 4이기 때문입니다.
출력 테이블의 모든 값에는 두 부분이 있습니다. 즉, 해당 꼭지점에 도달하는 데 드는 총 비용과 그 꼭지점에 대한 경로의 마지막 이웃입니다. 예를 들어, 꼭지점 C의 열에있는 값 4G는 C에 도달하는 데 드는 비용이 4이고 C에 대한 경로가 G를 통과한다는 것을 의미합니다. nil의 값은 해당 꼭지점에 대한 경로가 발견되지 않았음을 나타냅니다.
Third pass
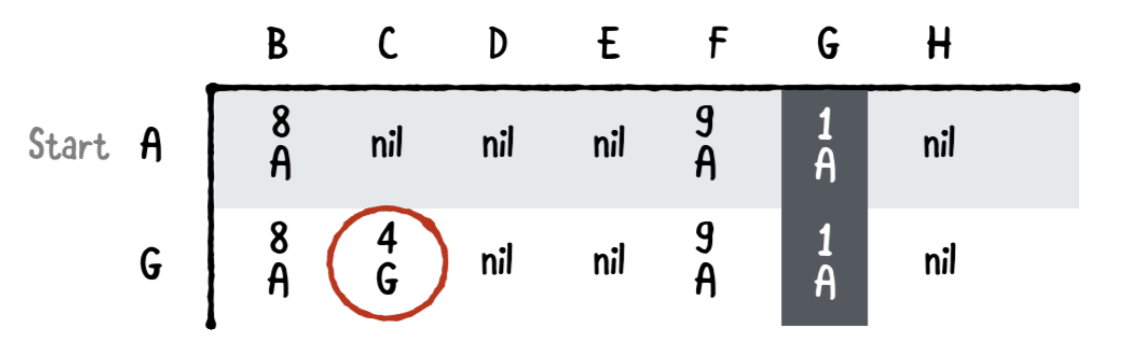
다음 싸이클에서, 다음으로 가장 낮은 값을 봅니다. 이 표에 따르면 C에 대한 경로가 가장 작은 비용을 가지므로 C에서 검색을 계속 진행됩니다. C에 도달하는 최단 경로를 찾았기 때문에 C열을 채웁니다.
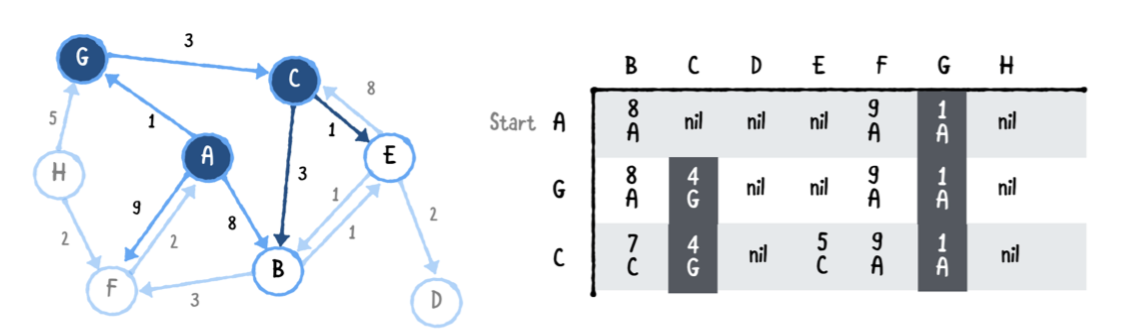
C가 가지고 있는 모든 모서리를 봅니다.
- C 에서 E는 총 4+1=5의 비용을 가집니다
- C 에서 B는 총 4+3=7의 비용을 가집니다.
B로 가는 가장 낮은 비용의 경로를 찾았습니다. 그리고 B의 이전값을 교체합니다.
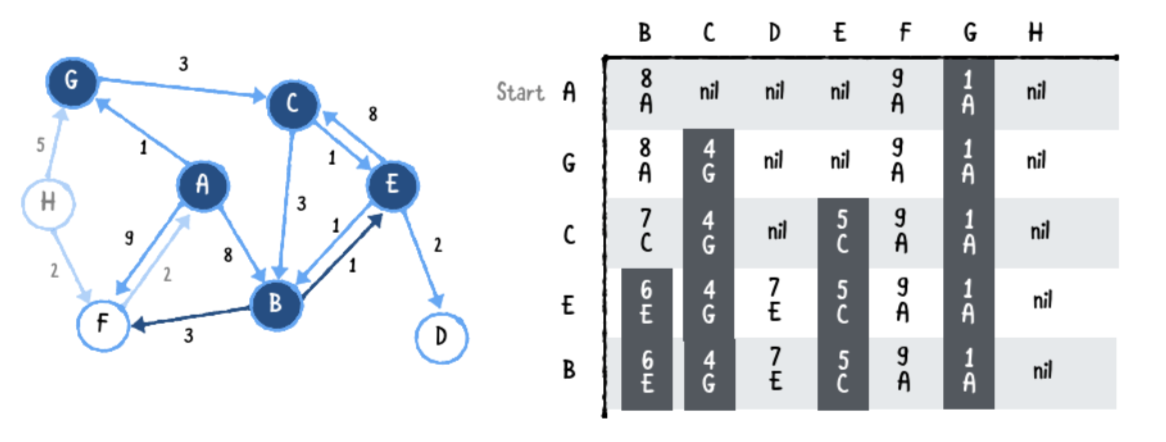
Fourth pass
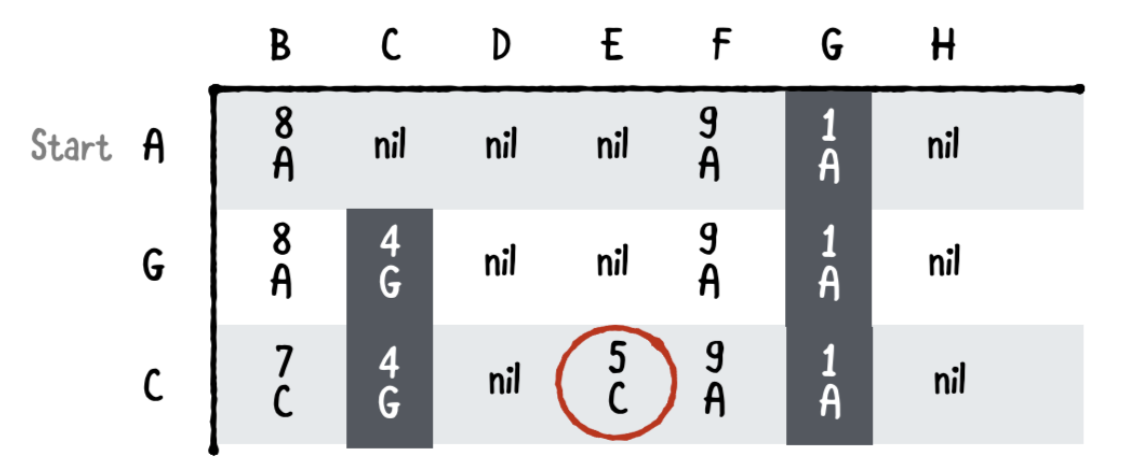
이제 다음 싸이클에서. 가장 낮은 비용의 경로가 무엇인지 자신에게 질문해봅니다. 이 표에 따름녀 C에서 E까지의 총 비용은 5 이므로 검색은 E에서 계속됩니다.
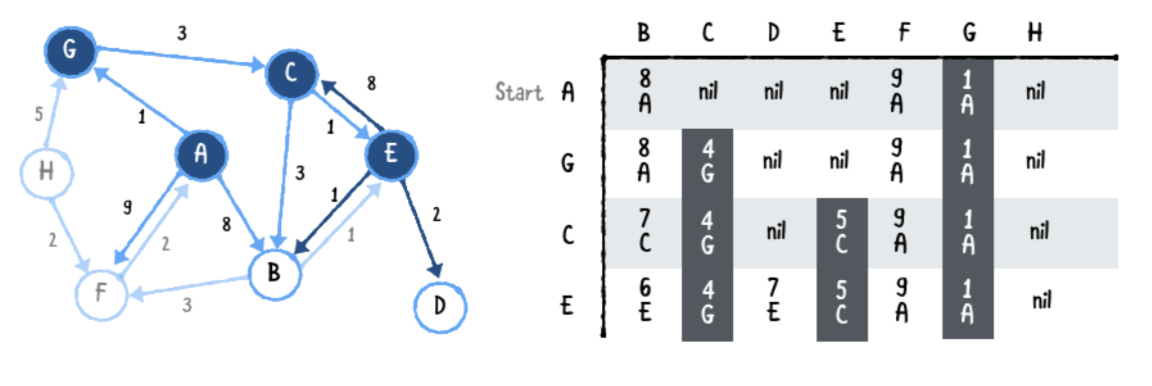
최단 경로를 찾았기 때문에 E 열을 채 웁니다. 꼭지점 E는 다음과 같은 가장자리를가집니다.
- B 에서 C는 5+8=13의 비용을 가집니다. C로 가는 가장 빠른 경로를 이미 찾았기때문에. 이 경로를 무시합니다.
- E 에서 D는 비용 7을 가집니다.
- E 에서 B는 5+1로 6의 비용을 가집니다. 테이블에 따르면 B로 가는 가장 짧은 비용은 7입니다. E에서 B로 가는 것이 가장 짧은 비용이므로 업데이트 합니다
Fifth pass
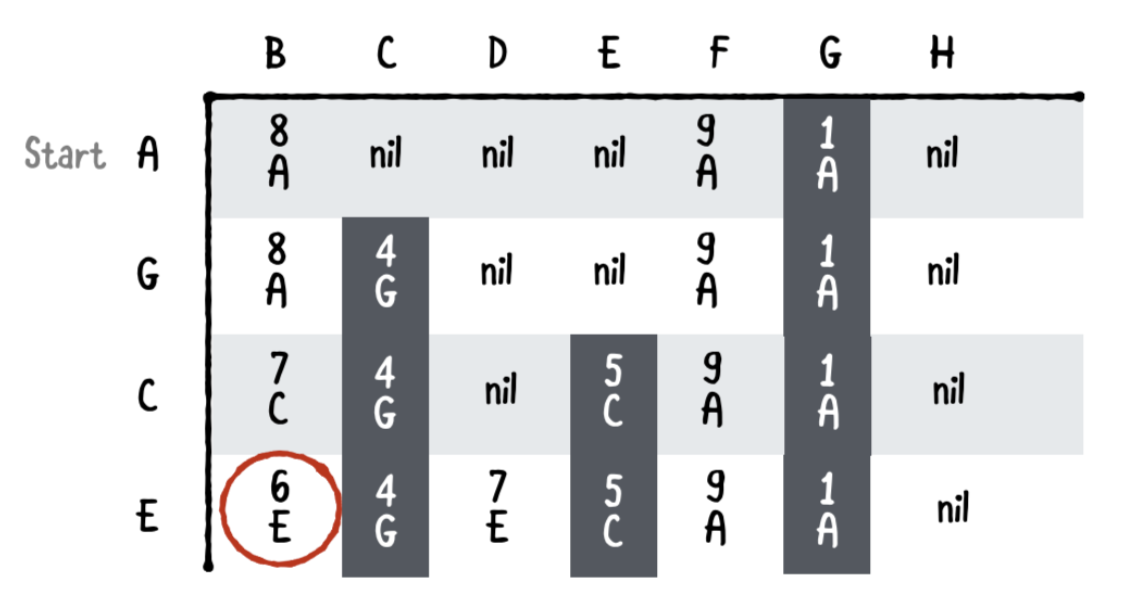
다음 B에서 계속 검색합니다.
B는 다음 모서리를 가집니다
- B에서 E는 6+1의 비용을 가지지만 이미 E로 가는 최단값을 알고 있기때문에 무시합니다.
- B에서 F는 6+3=9의 비용을 가집니다. 테이블에서 현재 경로 A에서 F까지는 9의 비용입니다. 더 짧지 않으므로 이 경로를 무시할 수 있습니다.
Sixth pass
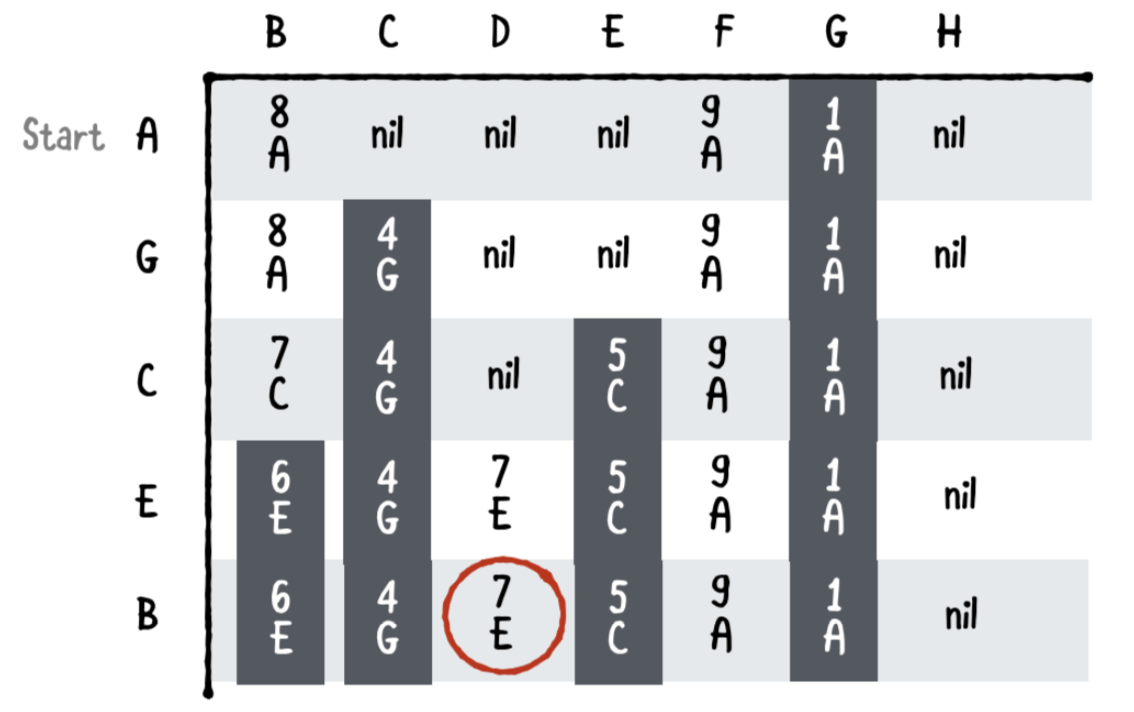
D에서 계속 검색합니다
그러나 D에는 모서리가 없으므로 막다른 길입니다. D에 대한 최단 경로를 기록하고 계속합니다.
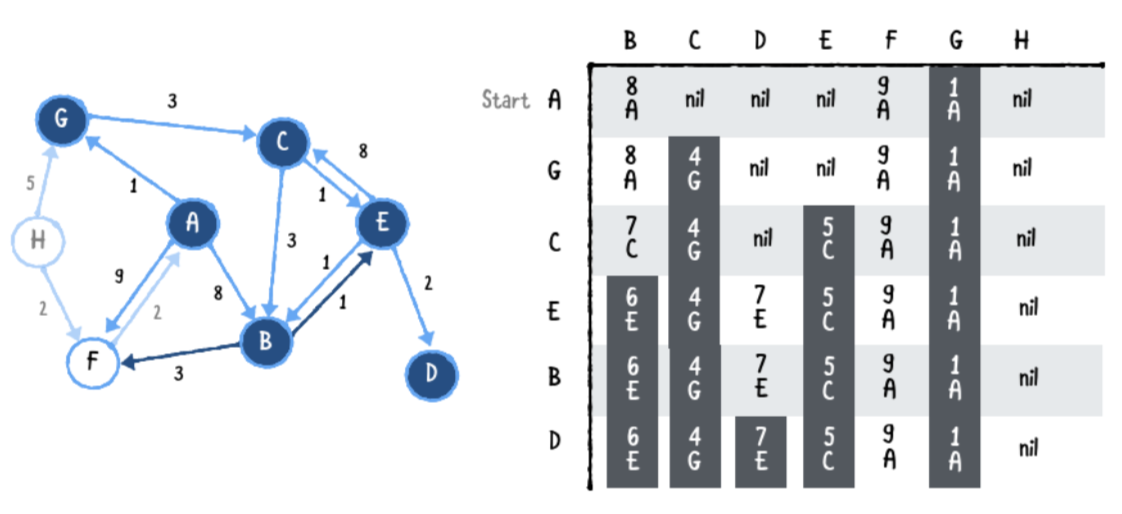
Seventh pass
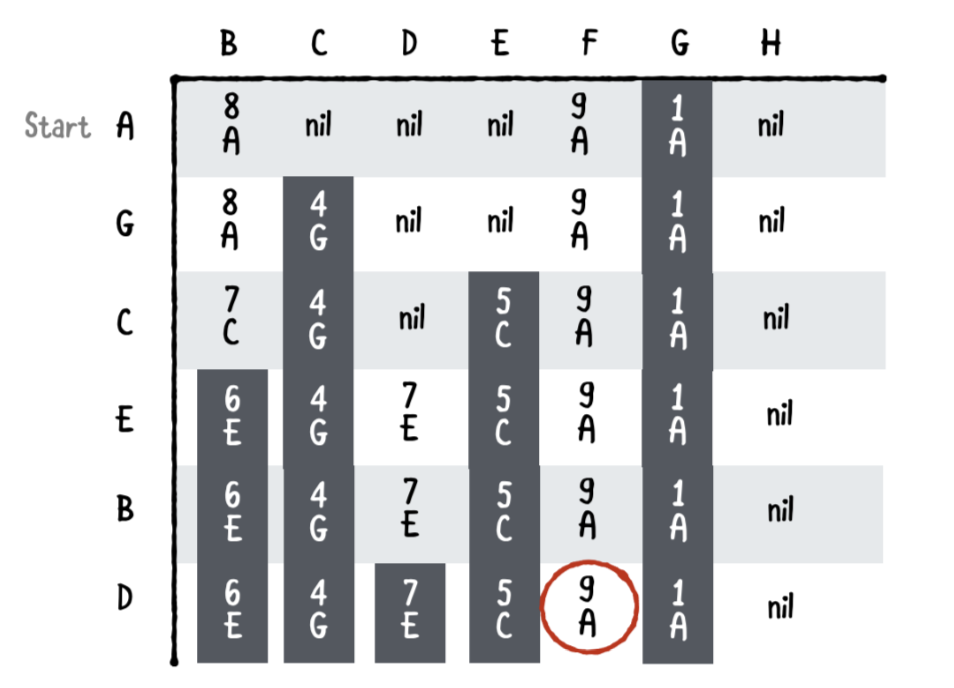
다음은 F 입니다.
F는 A로 가는 하나의 모서리를 가지고 있고 9+2=11의 비용을 가집니다. A는 시작 꼭지점이므로 이 값을 무시할수 있습니다.
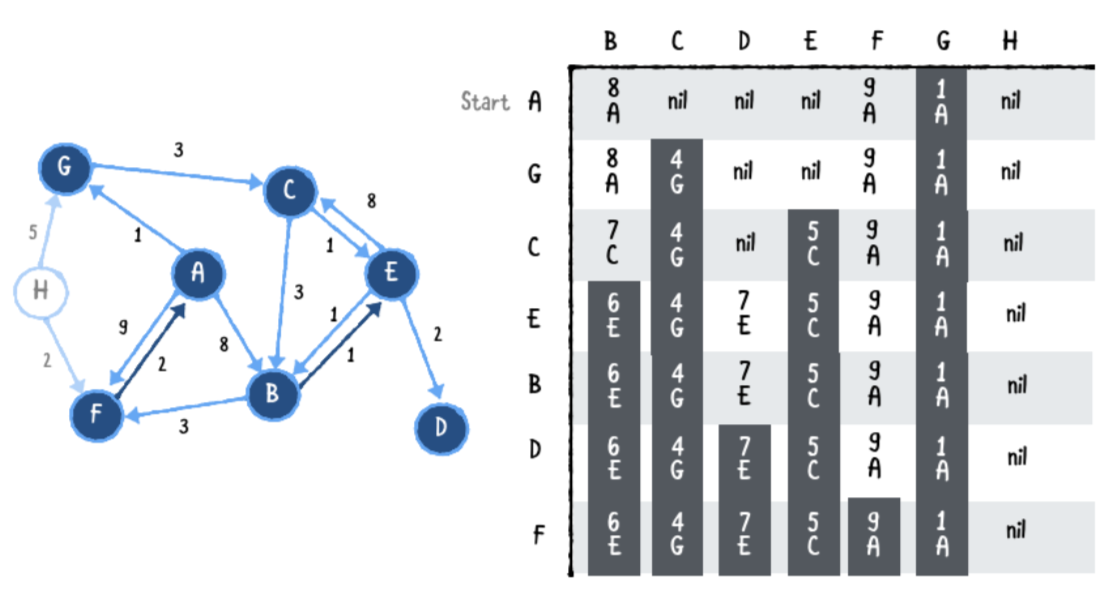
Eighth pass
H를 제외하고 모든 꼭지점을 방문 했습니다. H에는 G와 F에 두개의 방향이 있는 모서리가 있습니다. 그러나 A에서 H까지의 경로는 없습니다. 이 때문에 H의 전체열은 0 입니다.
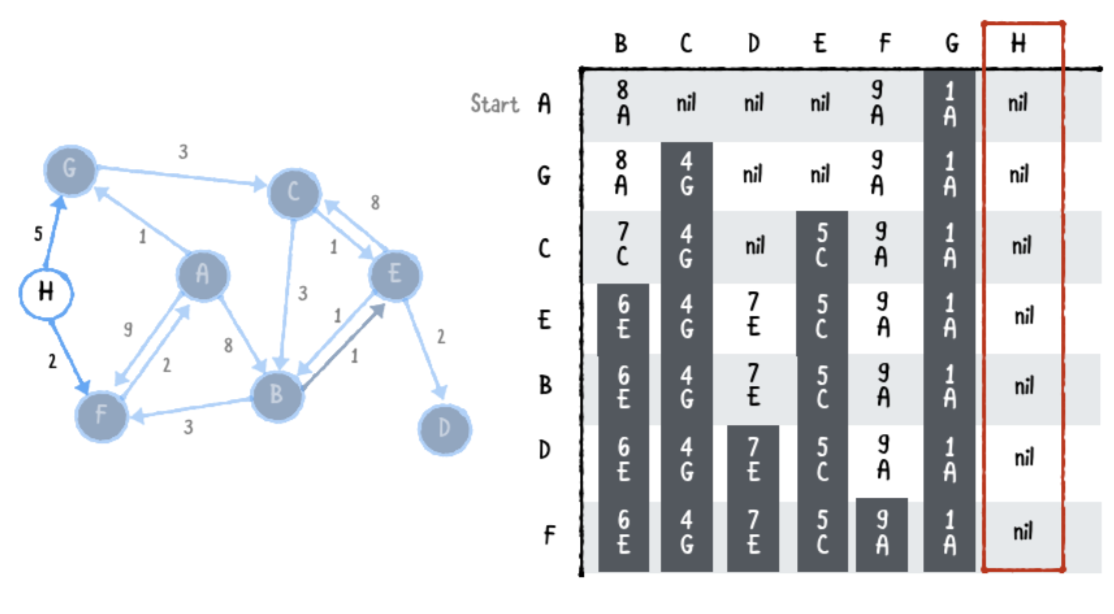
모든 꼭지점을 방문했으니 다익스트라의 알고리즘이 완성되었습니다~!
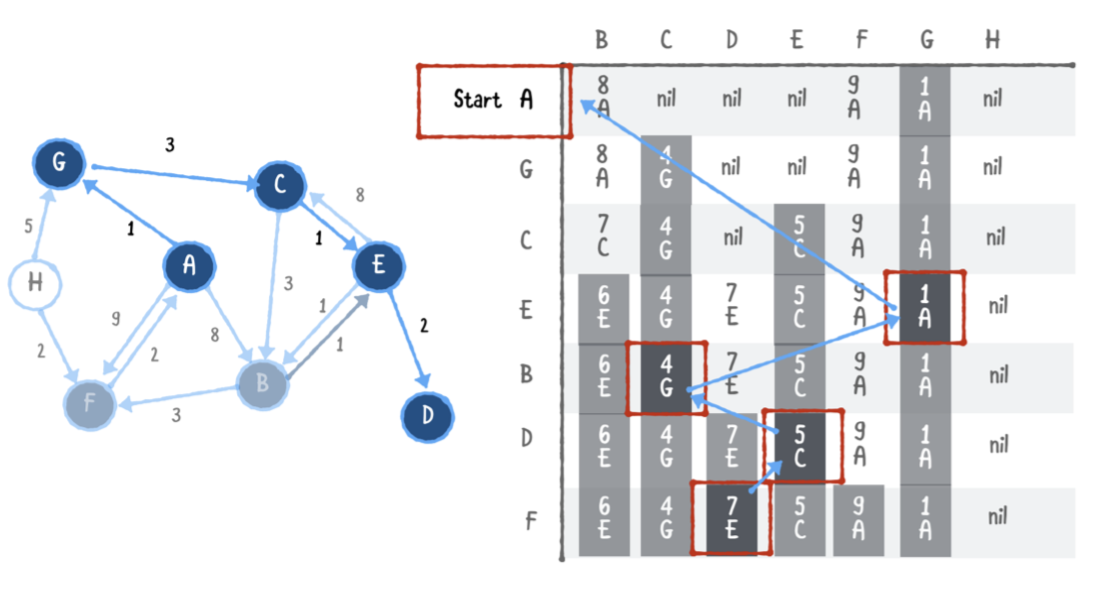
이제 최단 경로와 최종 비용을 확인할 수 있습니다. 예를 들어 D까지 도달하는데 드는 비용이 7임을 나타냅니다. 경로를 찾으려면 뒤로 이동하세요. 각 열은 현재 꼭지점과 연결된 이전 꼭지점을 기록합니다. D -> E -> C -> G -> A로 돌아가야합니다.
이것을 코드로 어떻게 만들 수 있는지 살펴봅니다
Implementation
Raywenderlich책에 나와있는 구현방식을 따르지 않고 다른 방법을 사용했습니다. 책에 있는 구현방식은 이해하기가 쉽지 않았고, 좀더 쉽게 이해할수 있는 방식으로 작성했습니다. 두 구현의 기본 원리는 같습니다.
Dijkstra Node
public class DijkstraNode<T: Equatable & Hashable>: Equatable {
// 값, 방문상태, 참조값 변수
public var value: T
public var edges: [DijkstraEdge<T>]
public var visited: Bool
// 출발지점에서 현재 노드에 이르는 최단 거리
public var distance: Int = Int.max
// 최단 경로에 이르는 기존의 노드
// 각 노드에 이르는 경로를 각 노드의 최단 경로로 저장해야 하기 위한 변수
public var previous: DijkstraNode<T>?
public init(value: T, edges: [DijkstraEdge<T>], visited: Bool) {
self.value = value
self.edges = edges
self.visited = visited
}
public static func == <T: Equatable> (lhs: DijkstraNode<T>, rhs: DijkstraNode<T>) -> Bool {
guard lhs.value == rhs.value else { return false }
return true
}
}
extension DijkstraNode: Hashable {
public var hashValue: Int {
get {
return value.hashValue
}
}
}
미방문 노드를 저장하기 위해 Set을 사용합니다. 이를 위해서는 먼저 노드에 Hashable, 그리고 Equatable프로토콜을 적용합니다.
각 노드에 이르는 임시 거리를 계산하기 위해 distance라 부르는 새로운 프로퍼티를 추가합니다. 위 코드에서는 Int.max로 distance변수를 초기화하는데, 이는 다이크스트라 알고리즘엣 ㅓ사용하는 무한값에 가까운 의미를 지닙니다.
Dijkstra Edge
public class DijkstraEdge<T: Equatable & Hashable>: Equatable {
public var from: DijkstraNode<T>
public var to: DijkstraNode<T>
public var weight: Double
public init(weight: Double, from: DijkstraNode<T>, to: DijkstraNode<T>) {
self.weight = weight
self.from = from
self.to = to
from.edges.append(self)
}
public static func == <T: Equatable> (lhs: DijkstraEdge<T>, rhs: DijkstraEdge<T>) -> Bool {
guard lhs.from.value == rhs.from.value else { return false }
guard lhs.to.value == rhs.from.value else { return false }
return true
}
}
extension DijkstraEdge: Hashable {
public var hashValue: Int {
let stringHash = "\(from.value)->\(to.value)"
return stringHash.hashValue
}
}
구현방식은 이전 포스트의 MST와 같습니다.
DijkstraGraph
// 다익스트라 알고리즘에 사용될 녀석.
public static func dijkstraPath(
startNode: DijkstraNode<T>,
graph: DijkstraGraph<T>,
finishNode: DijkstraNode<T>) {
// 모든 미방문 노드를 저장하기 위한 세트를 생성
var unvisitedNodes = Set<DijkstraNode<T>>(graph.nodes)
// 방문 표식을 남기고 임시 거리로 0을 입력
startNode.distance = 0
// 현제 노드를 할당
var currentNode: DijkstraNode<T> = startNode
// 마지막 노드를 방문할 때까지 반복합니다
while finishNode.visited == false {
// 각각의 미방문 이웃에 대해, 현재 노드와의 거리를 계산합니다.
for edge in currentNode.edges.filter({ $0.to.visited == false }) {
// 현재 노드와 그 이웃 노드의 임시 거리를 계산 합니다
let temporaryDistance = currentNode.distance + Int(edge.weight)
// 임시 거리가 현재 이웃과의 거리보다 작으면, 임시 거리로 업데이트 합니다. 해당 모서리의 이전 노드를 현재 노드로 업데이트 합니다.
if edge.to.distance > temporaryDistance {
edge.to.distance = temporaryDistance
edge.to.previous = currentNode
}
}
// 노드에 방문 표식을 남깁니다.
currentNode.visited = true
// 미 방문 노드 세트에서 현재 노드를 삭제 합니다
unvisitedNodes.remove(currentNode)
if let newCurrent = unvisitedNodes.sorted(by: { (nodeA, nodeB) -> Bool in
nodeA.distance < nodeB.distance
}).first {
currentNode = newCurrent
}else {
break
}
DijkstraGraph.printShortestPath(node: finishNode)
}
}
// 마지막값에 기록된 이전의 값들을 거꾸로 순회하며 찾아나감..
public static func printShortestPath(node: DijkstraNode<T>) {
if let previous = node.previous {
DijkstraGraph.printShortestPath(node: previous)
}else {
print("Shortest path: ")
}
print("-> \(node.value)", terminator:"")
}
}
- 미방문 노드 세트를 생성(노드를 초기화하면서 무한값을 거리로 설정)
- 현재 노드를 초기 노드로 설정합니다.
- 각각의 미방문 이웃에 다다르기 위한 최단 거리를 업데이트 합니다. 업데이트를 마치면, 기존의 노드 또한 업데이트해서 현재 노드에 이르기 위한 최단 경로를 추적하고, 현재의 노드에 방문 표식을 남깁니다.
- 거리값이 가장 낮은 다음 노드로 이동한 뒤, 마짐가 노드를 방문할 때 까지 3번 과정을 반복합니다.
- 마지막 노드에서 시작하는 최단 경로를 출력합니다
let nodeA = DijkstraNode(value: "A", edges: [], visited: false)
let nodeB = DijkstraNode(value: "B", edges: [], visited: false)
let nodeC = DijkstraNode(value: "C", edges: [], visited: false)
let nodeD = DijkstraNode(value: "D", edges: [], visited: false)
let nodeE = DijkstraNode(value: "E", edges: [], visited: false)
let nodeF = DijkstraNode(value: "F", edges: [], visited: false)
let nodeG = DijkstraNode(value: "G", edges: [], visited: false)
let nodeH = DijkstraNode(value: "H", edges: [], visited: false)
let edgeAB = DijkstraEdge(weight: 8, from: nodeA, to: nodeB)
let edgeAF = DijkstraEdge(weight: 9, from: nodeA, to: nodeF)
let edgeFA = DijkstraEdge(weight: 2, from: nodeF, to: nodeA)
let edgeAG = DijkstraEdge(weight: 1, from: nodeA, to: nodeG)
let edgeHG = DijkstraEdge(weight: 5, from: nodeH, to: nodeG)
let edgeHF = DijkstraEdge(weight: 2, from: nodeH, to: nodeF)
let edgeGC = DijkstraEdge(weight: 3, from: nodeG, to: nodeC)
let edgeBE = DijkstraEdge(weight: 1, from: nodeB, to: nodeE)
let edgeCB = DijkstraEdge(weight: 3, from: nodeC, to: nodeB)
let edgeCE = DijkstraEdge(weight: 1, from: nodeC, to: nodeE)
let nodeEC = DijkstraEdge(weight: 8, from: nodeE, to: nodeC)
let edgeED = DijkstraEdge(weight: 2, from: nodeE, to: nodeD)
let graph = DijkstraGraph(nodes: [nodeA, nodeB, nodeC, nodeD,
nodeE, nodeF, nodeG, nodeH])
DijkstraGraph.dijkstraPath(startNode: nodeA, graph: graph, finishNode: nodeD)
위 코드를 통해서 찾은 최단 거리는 -> A-> G-> C-> E-> D 입니다.
Reference
Data Structures and Algorithms in Swift
https://github.com/raywenderlich/swift-algorithm-club/tree/master/Dijkstra Algorithm