Swift, Data Structure, Heap

The heap property
Heap applications
Common heap operations
How do you represent a heap?
Removing from a heap
- Implementation of remove
Insertin into a heap
- Implementation of insert
Removing from an arbitrary index
Searching for an element in a heap
Building a heap
Testing
Reference

The Heap Data Structure

힙을 배열을 사용하고 구성하고, 이진 힙이라고도 하는 완전한 이진 트리(complete binary tree) 입니다.

힙은 두가지 특성을 가지고 있습니다

최대힙(Max heap): 가장큰값을 가진 요소는 가장 높은 우선순위를 가집니다.
최소힙(Min Heap): 가장 작은 값은 가진 요소는 가장 낮은 우선 순위를 가집니다.

The heap property

힙은 항상 만족해야만 하는 중요한 특성이 있습니다. 그것들은 힙 불변성(heap invariant) 또는 힙 고유특성(heap property)으로 알려져 있습니다.

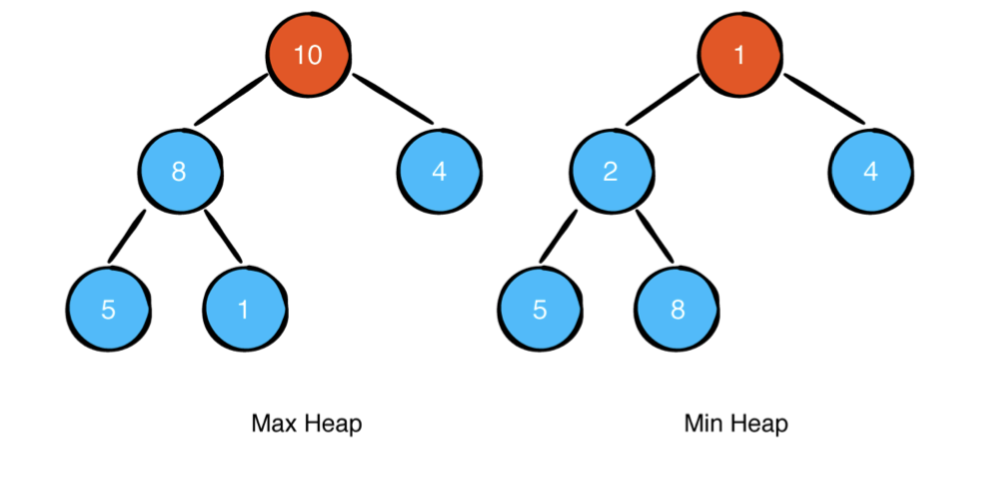
최대 힙에서 부모 노드는 항상 자식의 값보다 크거나 같은 값을 포함해야합니다. 루트 노드에는 항상 가장 높은 값이 포함됩니다.

최소 힙에서는 부모 노드가 항상 자식의 값보다 작거나 같은 값을 포함해야합니다. 루트 노드에는 항상 가장 낮은 값이 포함됩니다.

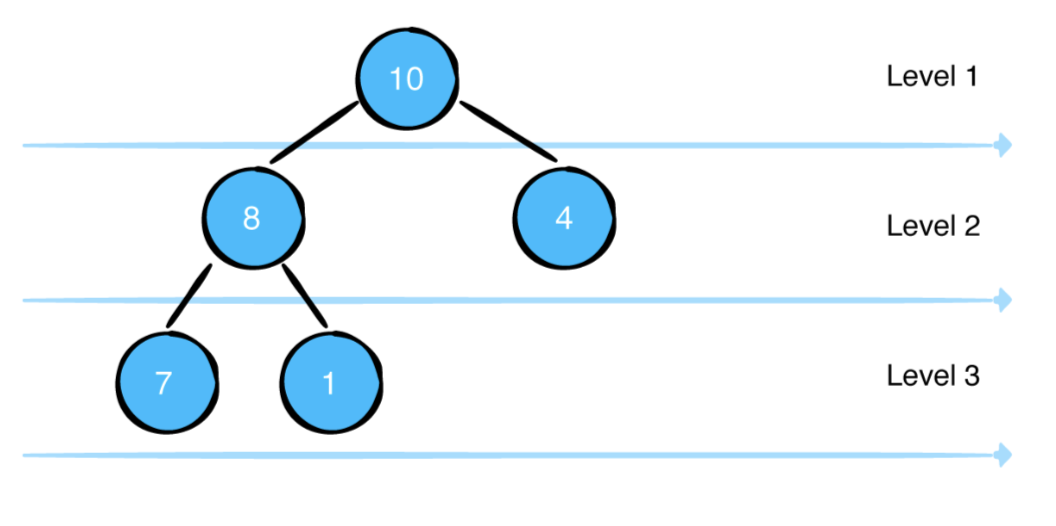
힙의 또 다른 중요한 특성은 완전한 이진 트리(complete binary tree)라는 것입니다. 즉, 마지막 레벨을 제외한 모든 레벨은 채워져 있어야 합니다.

Heap application

힙을 사용했을때 유용한 프로그램은 다음과 같습니다

컬렉션의 가장 낮은값 또는 가장 높은값의 연산
힙 정렬(Heap sort)
우선 순위 큐(Priority queue) 만들기
우선 순위 큐를 가진 Prim 또는 `Dijkstra와 같은 그래프 알고리즘 구축

Note: 이러한 Heap을 메모리 힙과 혼동하지마세요. 힙이라는 용어는 때로는 메모리 풀(memory pool)을 나타내기 위해 컴퓨터 과학에서 혼란스럽게 사용됩니다. 메모리 힙은 다른 개념이며 여기서는 공부 대상이 아닙니다

이 장에서는 컬렉션의 최소 및 최대 요소를 가져오는 것이 얼마나 편리한지 보여주는 힙(heap) 작성에 중점을 둡니다

Common heap operations

struct Heap<Element: Equatable> {
  var elements: [Element] = []
  let sort: (Element, Element) -> Bool
  init(sort: @escaping (Element, Element) -> Bool) {
    self.sort = sort
  }
}

이 유형에는 힙이 요소를 보유 할 배열과 힙을 정렬하는 방법을 정의하는 정렬 함수가 있습니다. 이 함수는 이니셜 라이저에 적절한 함수를 전달하여 min 및 max 힙을 만드는 데 사용할 수 있습니다.

How do you represent a heap?

트리는 자식에 대한 참조를 저장하는 노드를 포함합니다. 이진 트리의 경우 이들은 왼쪽 및 오른쪽 자식에 대한 참조로 표현합니다. 힙은 실제로 이진 트리이지만 간단한 배열로 표현할수 있습니다.

이것은 트리를 만드는 특별한 방법 처럼 보이지만. 이 힙 구현의 이점 중 하나는 힙의 요소가 모두 메모리에 저장 되므로 시간 효율성과 공간 복잡성의 이득입니다.

나중에 스왑 요소가 힙 작업에서 중요한 역할을 하게 됩니다. 또한 이진 트리 데이터 구조로 사용하는 것보다 배열을 사용하는 것이 더 쉽습니다.

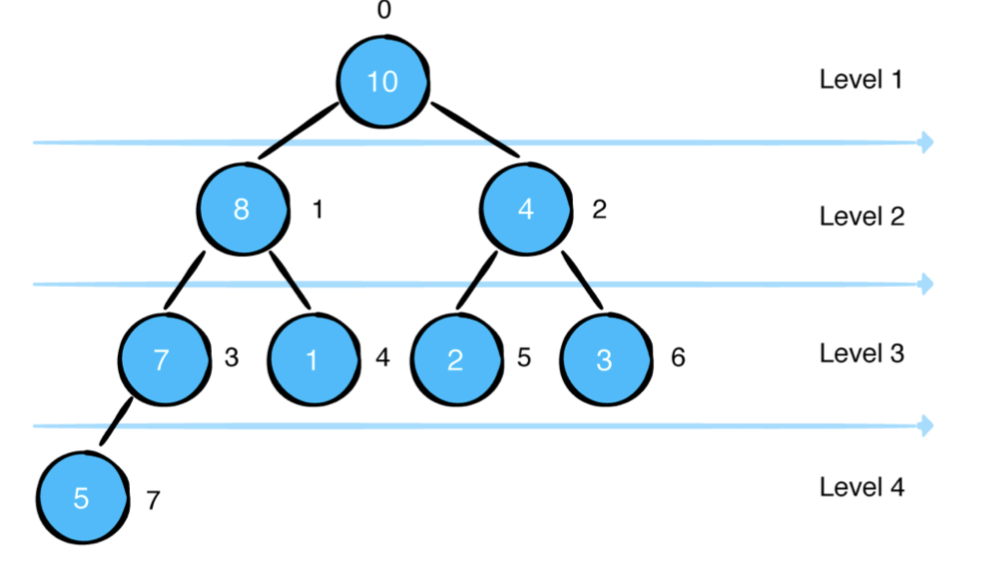
위의 힙을 배열로 나타내려면 각 요소를 순회하기 만하면됩니다. 왼쪽에서 오른쪽으로 레벨 별 레벨

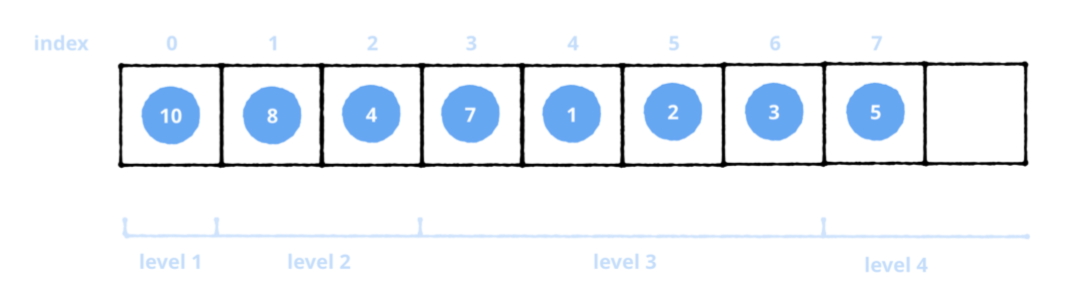
레벨을 올리면 이전 레벨보다 두 배 많은 노드가 생깁니다.

이제는 힙의 노드에 쉽게 액세스 할 수 있습니다. 이것을 배열의 요소에 액세스하는 방법과 비교할 수 있습니다. 왼쪽 또는 오른쪽 분기를 가로 지르지 않고 간단한 수식을 사용하여 배열의 노드에 액세스하면됩니다.

0부터 시작하는 인덱스 i에서 노드가 주어진 경우 :

이 노드의 왼쪽 자식은 인덱스 2i + 1에서 찾을 수 있습니다.
이 노드의 오른쪽 자식은 인덱스 2i + 2에서 찾을 수 있습니다.
0은 root node

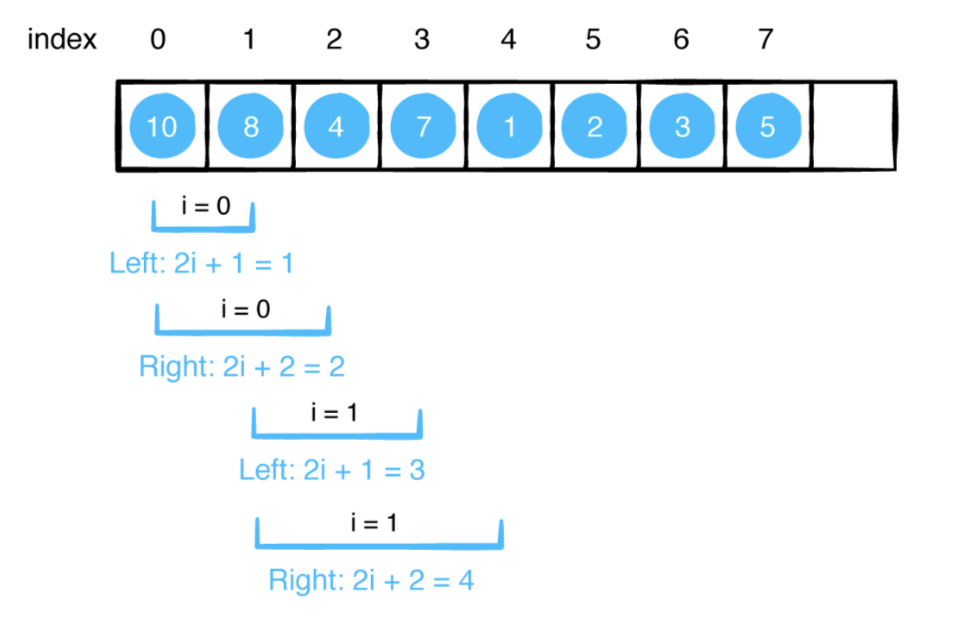
노드의 부모를 얻을 수도 있습니다. 이 경우 i를 해결할 수 있습니다. 인덱스 i에있는 자식 노드가 주어지면 이 자식 노드의 부모 노드는 자식노드 에서 ((i-1) / 2) 수식으로 찾을 수 있습니다.

참고 : 노드의 왼쪽 및 오른쪽 자식을 가져 오기 위해 실제 트리를 가로 지르는 작업은 O(log n) 작업입니다. 배열과 같은 임의 액세스 데이터 구조에서 동일한 작업은 O(1)입니다.

다음으로 편의 연산자들을 추가합니다

var isEmpty: Bool {
  return elements.isEmpty
}
var count: Int {
  return elements.count
}
func peek() -> Element? {
  return elements.first
}
func leftChildIndex(ofParentAt index: Int) -> Int {
  return (2 * index) + 1
}
func rightChildIndex(ofParentAt index: Int) -> Int {
  return (2 * index) + 2
}
func parentIndex(ofChildAt index: Int) -> Int {
  return (index - 1) / 2
}

Removing from a heap

기본 제거 작업은 단순히 힙에서 루트 노드를 제거합니다. 최대 힙을 가져와서 예시를 설명합니다.

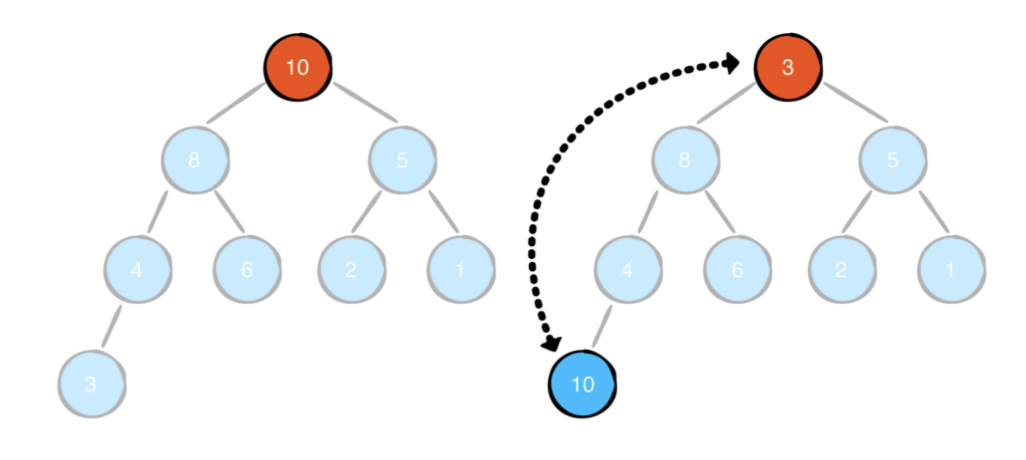
제거 작업은 루트 노드에서 최대 값을 제거합니다. 이렇게하려면 먼저 힙의 마지막 요소로 루트 노드를 바꿔야합니다.

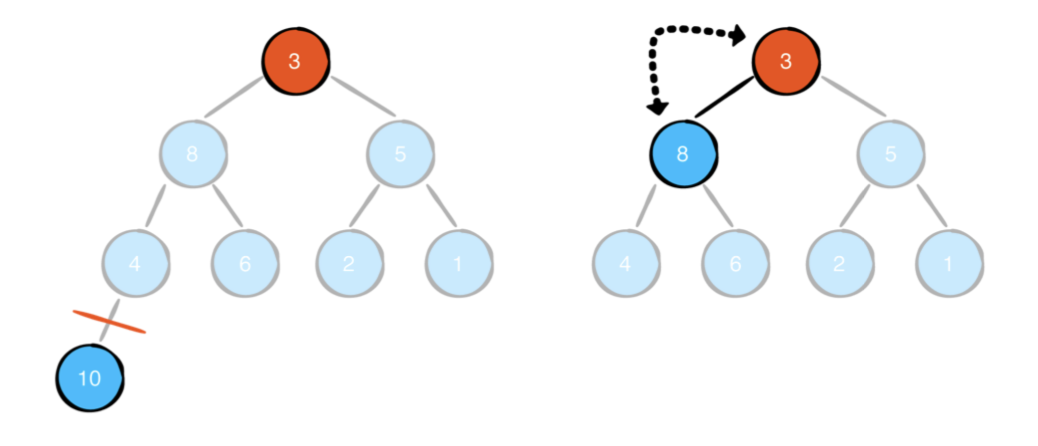
두 요소를 서로 바꾼 후에는 마지막 요소를 제거하고 나중에 값을 저장할 수 있습니다.

이제 최대 힙의 무결성을 확인해야합니다. 이 힙은 여전히 최대 힙의 조건에 부합하나요?

Note: 최대 힙에 대한 규칙은 모든 부모 노드의 값이 해당 자식 값보다 크거나 같아야한다는 것입니다. 힙이 이 규칙을 더 이상 따르지 않습니다. 따라서 sift down(=걸러내다 그런의미인듯...) 해야합니다.

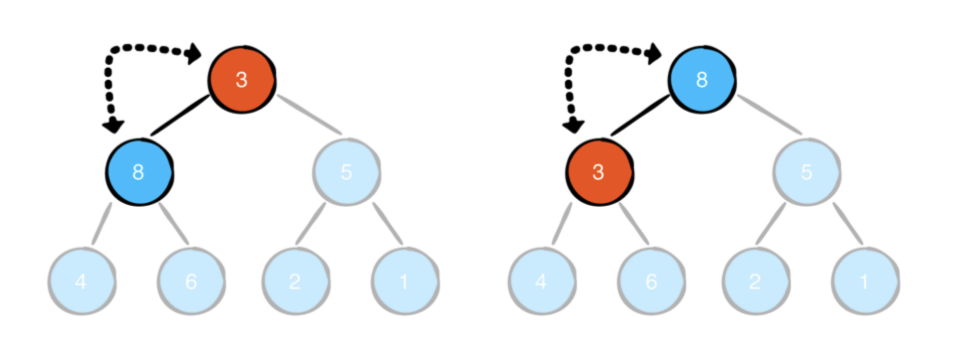
sift down을 수행하려면 현재 값 3부터 시작하여 왼쪽 및 오른쪽 하위를 확인합니다. 자식 중 하나에 현재 값보다 큰 값이 있으면 부모의 값과 바꿉니다. 두 자녀 모두 더 큰 값을가지고 있는 경우 큰 값을 가진 자녀와 부모를 바꿉니다.

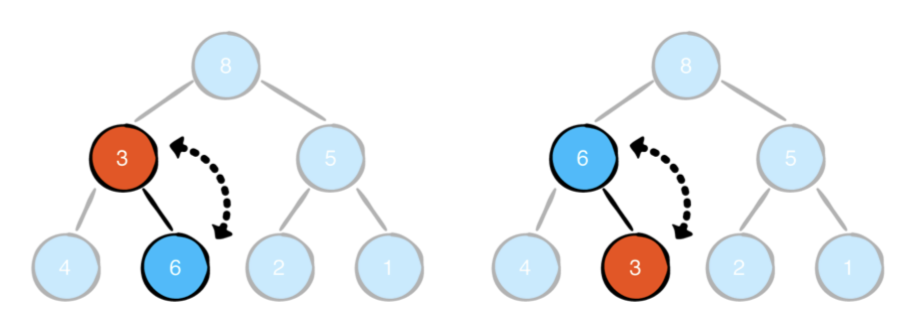
이제 노드의 값이 자식 값보다 크지 않을 때까지 계속 탐색해야합니다.

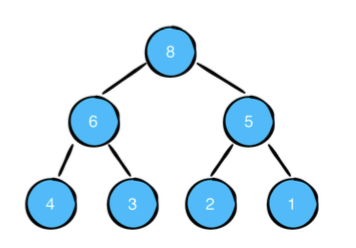
끝에 도달하면, 작업이 완료되고 최대힙 조건에 부합합니다.

Implementation of remove

mutating func remove() -> Element? {
  guard !isEmpty else { // 1
return nil
  }
  elements.swapAt(0, count - 1) // 2
  defer {
    siftDown(from: 0) // 4
  }
  return elements.removeLast() // 3
}

이 방법은 다음과 같습니다.

힙이 비어 있는지 확인하십시오. 그럴 경우 nil을 리턴하십시오.
힙의 마지막 요소로 루트를 스왑하십시오.
마지막 요소 (최대 값 또는 최소값)를 제거하고 반환하십시오.
힙은 더 이상 최대 또는 최소 힙이 될 수 없으므로 규칙을 준수하는지 확인하기 위해 선별 작업을 수행해야합니다.

mutating func siftDown(from index: Int) {
  var parent = index // 1
  while true { // 2
    let left = leftChildIndex(ofParentAt: parent) // 3
    let right = rightChildIndex(ofParentAt: parent)
    var candidate = parent // 4
    if left < count && sort(elements[left], elements[candidate]) {
      candidate = left // 5
    }
    if right < count && sort(elements[right], elements[candidate]) {
      candidate = right // 6
    }
    if candidate == parent {
return // 7 }
    elements.swapAt(parent, candidate) // 8
    parent = candidate
  }
}

Complexity : remove()의 전체적인 시간 복잡성은 O(log n)입니다. 배열에서 요소를 교환하는 것은 O(1) 만 사용하는 반면 힙의 요소를 이동 시키려면 O(log n) 시간이 걸립니다.

Inserting into a heap

아래의 heap의 값에 7을 삽입한다고 가정합니다.

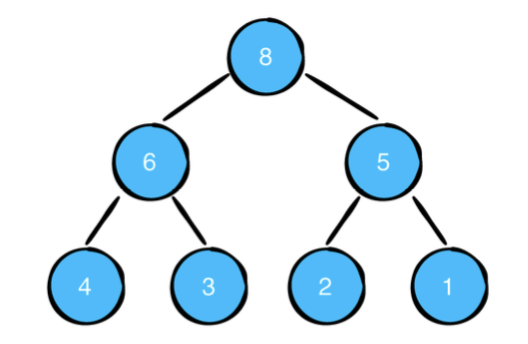
첫번째로 힙의 맨 끝에 값을 추가합니다.

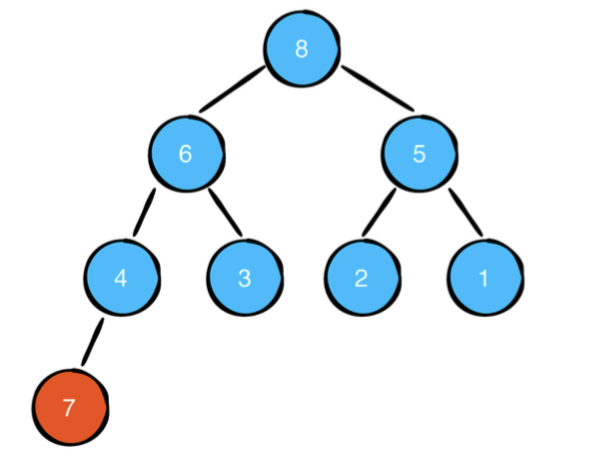
이제 최대 힙의 속성을 확인해야합니다. 아래로 내려가는 대신, 방금 삽입 한 노드가 부모보다 높은 우선 순위를 가질 수 있으므로 이제 위로 올라 가야합니다.

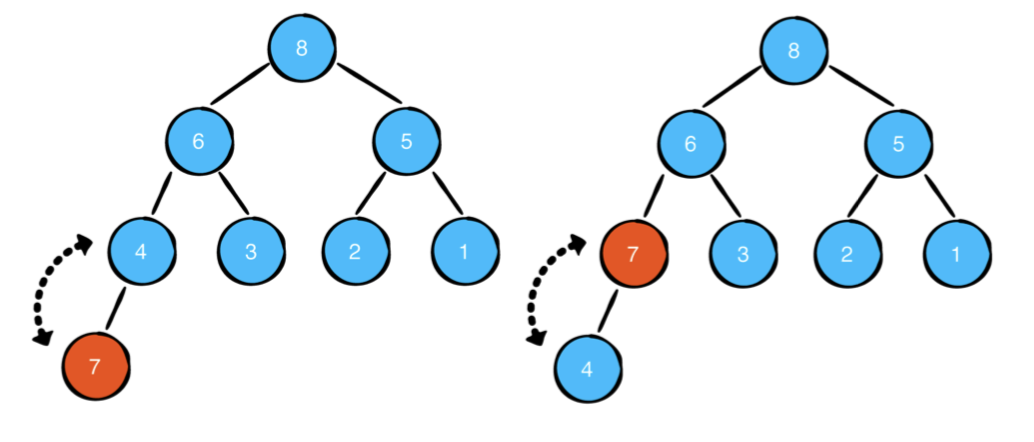
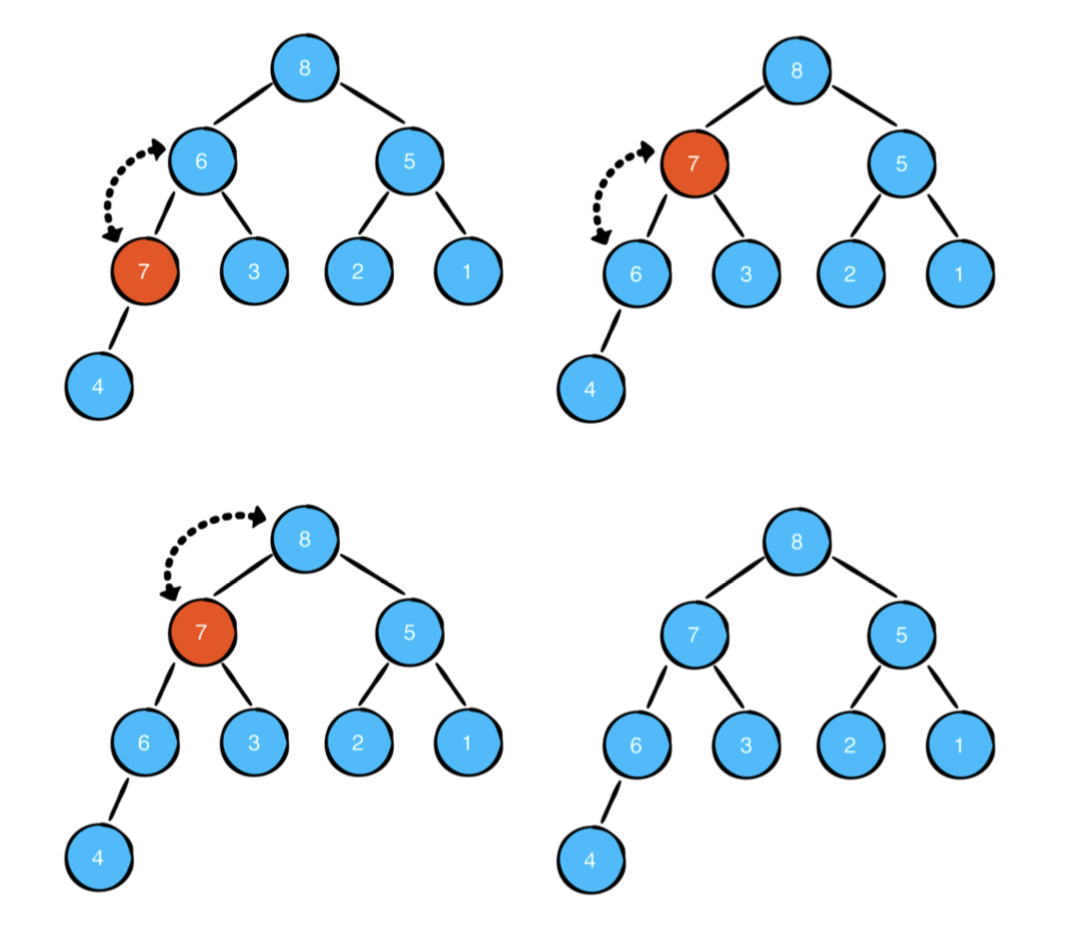
이제 maxHeap 조건을 만족합니다

Implementation of insert

mutating func insert(_ element: Element) {
  elements.append(element)
  siftUp(from: elements.count - 1)
}
mutating func siftUp(from index: Int) {
  var child = index
  var parent = parentIndex(ofChildAt: child)
  while child > 0 && sort(elements[child], elements[parent]) {
    elements.swapAt(child, parent)
    child = parent
    parent = parentIndex(ofChildAt: child)
    }
}

보시다시피 구현은 매우 간단합니다.

insert는 요소를 배열에 추가 한 다음 위로 이동합니다.
siftUp은 현재 노드를 부모 노드보다 우선 순위가 높은 노드로 바꿉니다.

Complexity : Insert(_ :)의 전체적인 시간 복잡성은 O(log n)입니다. 배열에 요소를 추가하는 것은 O(1) 이지만 힙에 요소를 추가할땐 O(log n)의 시간복잡성을 가지게 됩니다.

Removing from an arbitrary index

mutating func remove(at index: Int) -> Element? {
  guard index < elements.count else {
    return nil // 1
  }
  if index == elements.count - 1 {
    return elements.removeLast() // 2
  } else {
    elements.swapAt(index, elements.count - 1) // 3
    defer {
      siftDown(from: index) // 5
      siftUp(from: index)
    }
    return elements.removeLast() // 4
  }
}

힙에서 요소를 제거하려면 색인이 필요합니다. 어떻게 작동하는지 살펴 보겠습니다.

인덱스가 배열 범위 내에 있는지 확인하십시오. 그렇지 않으면 nil을 리턴하합니다.
힙에서 마지막 요소를 제거하는 경우 특별한 작업을 수행 할 필요가 없습니다. 요소를 제거하고 반환하면됩니다.
마지막 요소를 제거하지 않으려면 먼저 요소를 마지막 요소로 바꿉니다. 요소.
그런 다음 마지막 요소를 반환하고 제거 합니다.
마지막으로, 힙의 특성을 조정하기 sift down 과 sift up을 수행합니다.

그러나 여기서 궁금증이 생깁니다 왜 sift down 과 sift up 두가지 경우를 수행하는지?

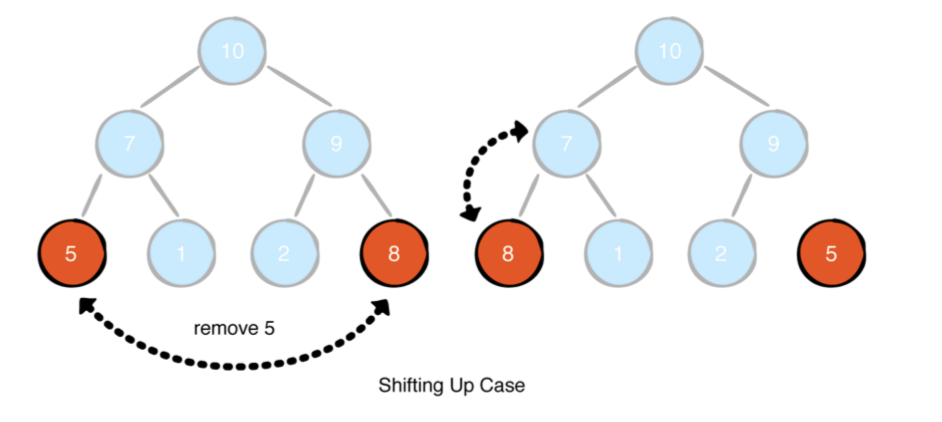
5를 제거하려고한다고 가정하세요. 5를 마지막 요소 인 8로 바꿉니다. 이제 최대 힙 속성을 충족시키기 위해 sift up 해야합니다.

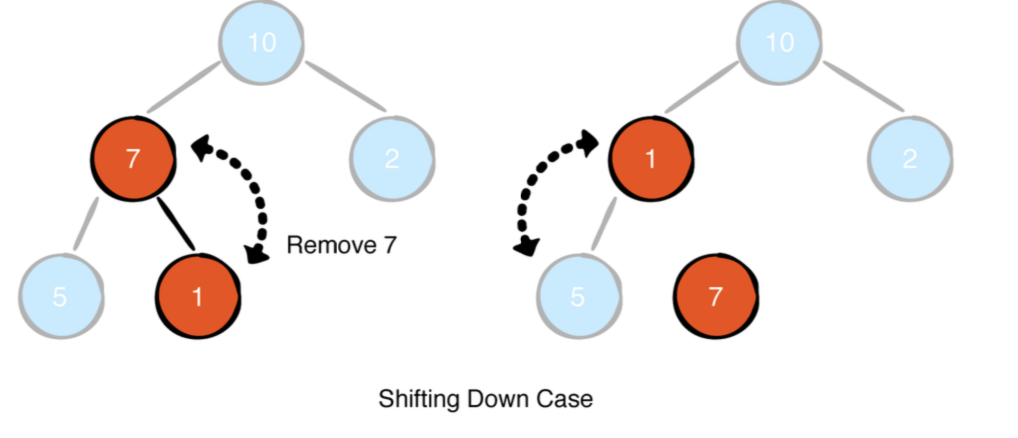
7을 제거하려고한다고 가정하십시오. 당신은 7을 마지막 요소와 교환하고, 이제 최대힙 속성을 충족 시키기 위해 sift down을 수행해야 합니다.

힙에서 임의의 요소를 제거하는 작업은 O(log n) 입니다. 그러나 어떻게 실제로 삭제하려는 요소의 색인을 찾나요?

func index(of element: Element, startingAt i: Int) -> Int? {
    if i >= count {
      return nil
    }
    if sort(element, elements[i]) {
      return nil
    }
    if element == elements[i] {
      return i
    }
    if let j = index(of: element, startingAt: leftChildIndex(ofParentAt: i)) {
      return j
    }
    if let j = index(of: element, startingAt: rightChildIndex(ofParentAt: i)) {
      return j
    }
    return nil
  }

building a heap

init(sort: @escaping (Element, Element) -> Bool,
     elements: [Element] = []) {
  self.sort = sort
  self.elements = elements
  if !elements.isEmpty {
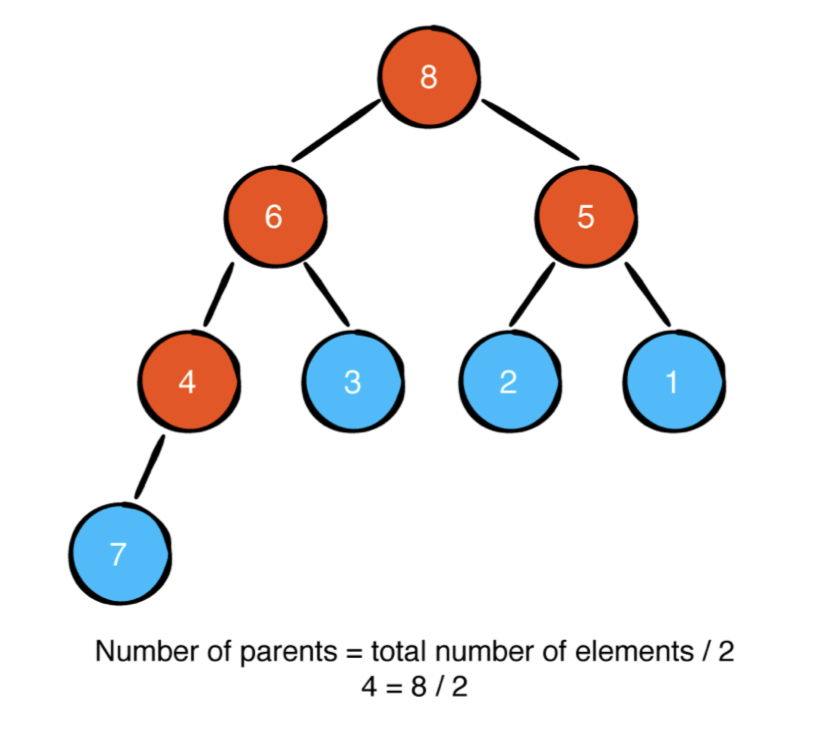
    for i in stride(from: elements.count / 2 - 1, through: 0, by: -1) {
      siftDown(from: i)
    }
	} 
}

Testing

var heap = Heap(sort: >, elements: [1,12,3,4,1,6,8,7])
while !heap.isEmpty {
  print(heap.remove()!)
}

전체 코드 주소

Reference

swift-algorithm-club/Heap
Data Structures and Algorithms in Swift

Swift, Data Structure, Heap

메모리의 Heap이 아닌 자료구조의 Heap을 알아보자!

Swift, Data Structure, Heap

메모리의 Heap이 아닌 자료구조의 Heap을 알아보자!

Contents

The Heap Data Structure

The heap property

Heap application

Common heap operations

How do you represent a heap?

Removing from a heap

Implementation of remove

Inserting into a heap

Implementation of insert

Removing from an arbitrary index

building a heap

Testing

Reference