Swift, Data Structure, AVL Trees

AVL Trees
Understanding balance
- Perfect balance
- “Good-enough” balance
- Unbalanced
Implementation
- Mersuring balance
- Rotations
- Left rotation
- Right Rotation
- Right-left rotation
- left-right rotation
- Balance
- Revisiting insertion
- Revisiting Remove
  - Test
더 알아보면 좋은것들
Reference

AVL Trees

자가 이진 균형 트리(self-balancing binary search tree)인 AVL Tree에 대해서 알아봅니다.

Understanding balance

균형잡힌 트리는 이진트리의 수행 능력을 최적화하는 중요한 열쇠입니다. 다음 주요한 세가지 균형 상태에 대해서 알아봅니다

Perfect balance

이진 검색 트리의 가상의 모형은 완전하게 균형된(perfectly balanced) 상태 입니다. 전문 용어로 트리의 모든 레벨이 위에서 아래로 채워져 있다는걸 의미합니다.

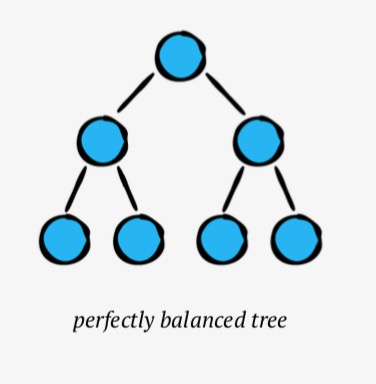
“Good-enough” balance

완벽한 균형을 달성하는 것이 이상적이지만, 거의 불가능합니다. 완벽하게 균형 잡힌 트리는 모든 레벨을 바닥에 채우는 정확한 노드 수를 포함해야하므로 특정 수의 요소만으로 완벽 할 수 있습니다.

예를 들어 1, 3 또는 7 노드가있는 트리는 완벽하게 균형을 맞출 수 있지만 트리의 마지막 레벨이 채워지지 않으므로 2, 4, 5 또는 6 트리는 완벽하게 균형을 유지할 수 없습니다.

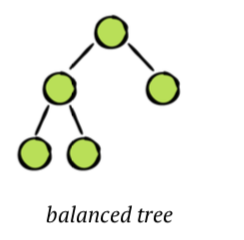
균형 잡힌 트리의 정의는 단말노드의 레벨을 제외하고 트리의 모든 레벨을 채워야한다는 것입니다. 대부분의 경우 이진 트리가 가장 좋은 방법입니다.

Unbalanced

마지막으로 불균형 상태가 있습니다. 이 상태의 이진 검색 트리는 불균형의 정도에 따라 다양한 수준의 성능 손실을 겪습니다.

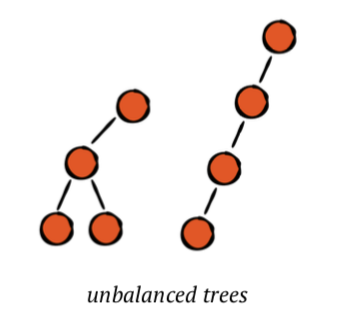
트리의 균형을 유지하면 찾기, 삽입 및 제거 작업에 O(log n) 시간의 복잡도가 부여됩니다. AVL 트리는 트리가 불균형 해지면 트리 구조를 조정하여 균형을 유지합니다.

Implementation

이진 탐색 트리와 AVL 트리는 동일한 구현의 대부분을 공유합니다.

Mersuring balance

이진 트리를 균형있게 유지하려면 트리의 균형을 측정하는 방법이 필요합니다. AVL 트리는 각 노드의 height 속성으로 이를 수행합니다. tree-speak에서 노드의 높이는 현재 노드에서 리프 노드까지의 최장 거리입니다.

public var height = 0 

특정 노드가 균형을 유지하는지 여부를 결정하기 위해 노드의 하위 노드의 상대적 높이를(relative height of a node’s children) 사용합니다.

각 노드의 왼쪽과 오른쪽 하위 노드의 높이는 기껏 해봐야 1 이하로(범위= -1 ~ 1) 차이가 나야 합니다. 이것은 balance factor 알려져 있습니다.

public var balanceFactor: Int {
  return leftHeight - rightHeight
}
public var leftHeight: Int {
  return leftChild?.height ?? -1
}
public var rightHeight: Int {
  return rightChild?.height ?? -1
}

balanceFactor는 왼쪽과 오른쪽 자식의 높이 차이를 계산합니다. 특정 자식이 nil 이면 높이는 -1로 간주됩니다.

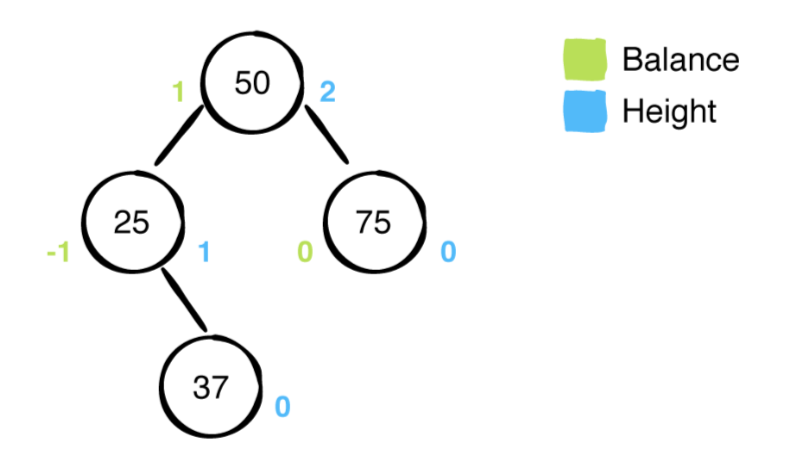
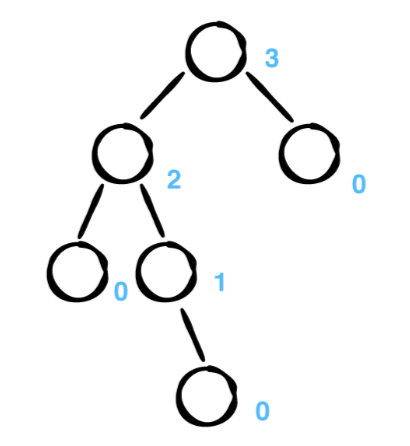
위는 균형잡힌 트리 입니다. 여기서는 리프노드를 제외한 모든 레벨이 채워집니다. 파란색 숫자는 각 노드의 높이를 나타내며 녹색 숫자는 balanceFactor를 나타냅니다.(이유는, 각 노드의 balanceFactor 값이 -1~1의 범위 안에 있기 때문. 해당 balanceFactor를 벗어나면 회전하여 균형을 맞추기때문!)

다음은 40 개의 다이어그램이 삽입 된 업데이트 다이어그램입니다.

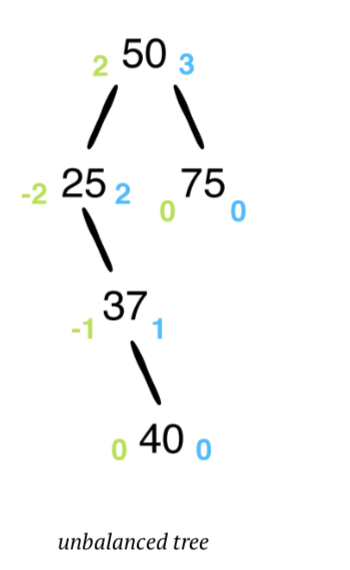
트리에 40값을 넣으면 언밸런스 트리로 바뀝니다. balanceFactor가 어떻게 변하는지 주목하세요. balanceFactor가 2 또는 -2 인 경우 불균형 트리가 표시됩니다.

두 개 이상의 노드가 잘못된 밸런싱 요소를 가질 수 있지만 잘못된 밸런스 요소가 포함 된 맨 아래 노드 (25가 포함 된 노드)에서 균형 조정 절차를 수행하기 만하면됩니다. 해당 지점이 회전을 수행하는 곳입니다.

Rotations

이진 검색 트리의 균형을 맞추는데 사용되는 절차를 회전이라고 합니다. 트리가 불균형해질수 있는 4가지 다른 방법으로 총 4개의 회전이 있습니다.

이는 왼쪽 회전(left rotation), 왼쪽-오른쪽 회전(left-right rotation), 오른쪽 회전(right rotation), 오른쪽-왼쪽 회전(right-left rotation)이 있습니다.

Left rotation

트리에 40을 넣어서 생긴 불균형 케이스는 left rotation으로 해결할수 있습니다. 일반적으로 노드 x의 왼쪽 회전은 다음과 같은 보입니다.

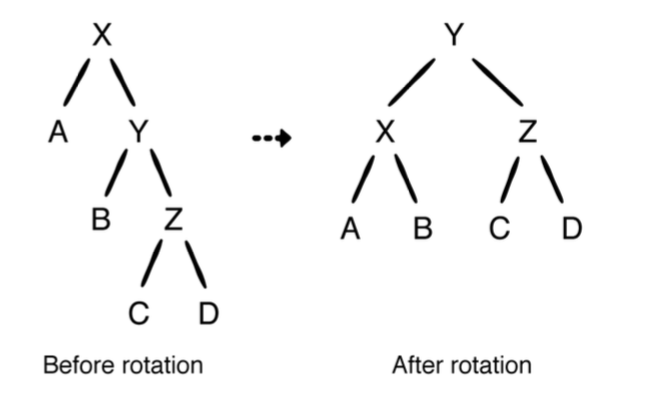
구체적으로 가기전에 두가지를 비교해야합니다.

이러한 노드에 대한 중위 순회(In-order traversal)은 동일하게 유지 됩니다
트리의 깊이(depth)는 회전후 1레벨만큼 감소합니다.

private func leftRotate(_ node: AVLNode<Element>) -> AVLNode<Element> {
        // 1. leftRotation시, 중심 노드
        let pivot = node.rightChild!
        // 2. 회전이후, 노드의 오른쪽 자식 노드는, pivot노드 보다 작으면서, node보다는 큰 값을 가진 노드를 반환
        node.rightChild = pivot.leftChild
        // 3. pivot의 왼쪽 자식으로 불균형 노드를 회전
        pivot.leftChild = node
        // 4 node, pivot의 height 재측정
        node.height = max(node.leftHeight, node.rightHeight) + 1
        pivot.height = max(pivot.leftHeight, pivot.rightHeight) + 1
        // 5. node의 위치와, hegiht 값 변환후, pivot 반환
        return pivot
    }

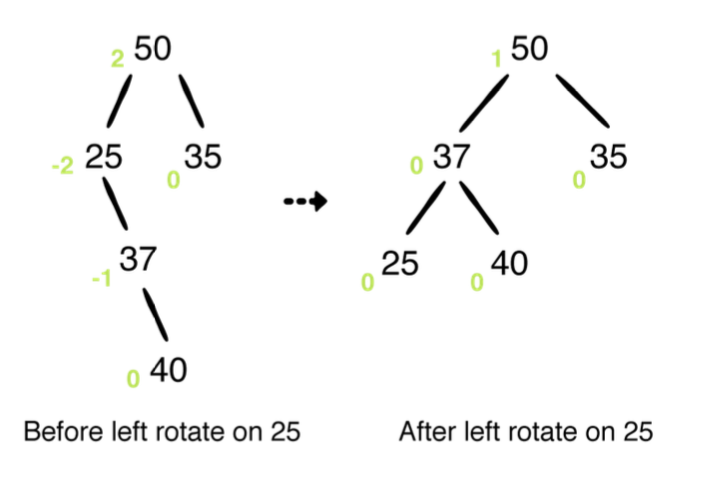
Right Rotation

오른쪽 회전은 왼쪽 회전의 데칼코마니 버전입니다. 왼쪽 자식이 불균형에 원인일때 오른쪽 회전을 사용할때 입니다. 일반적으로 오른쪽 회전은 다음과같이 보입니다.

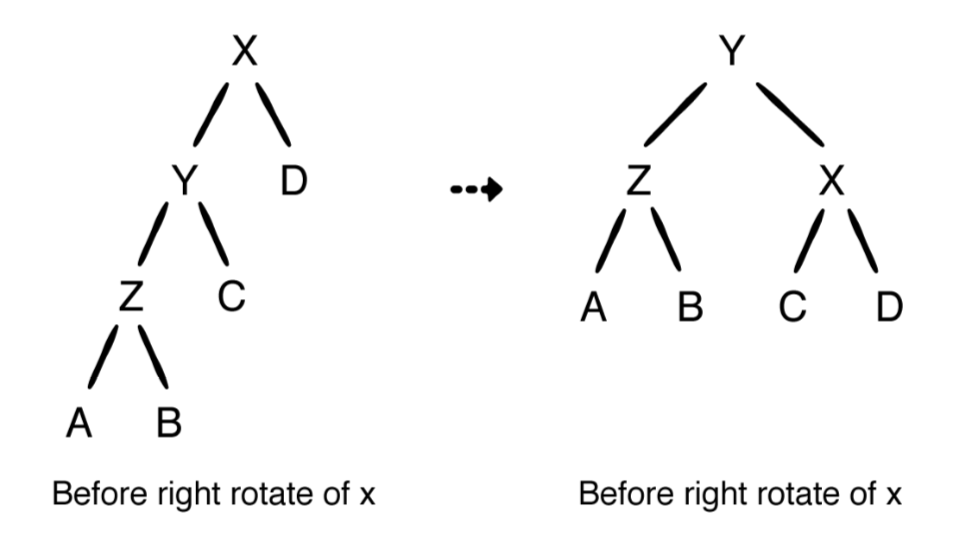
왼쪽 및 오른쪽 자식에 대한 참조가 바뀌었다는 점을 제외하면 leftRotate 구현과 거의 같습니다.

Right-left rotation

왼쪽 및 오른쪽 회전은 모두 왼쪽 자식 또는 모든 오른쪽 자식 노드의 균형을 맞출 수 있습니다. 원래 예제 트리에 36이 삽입 된 경우를 고려하십시오.

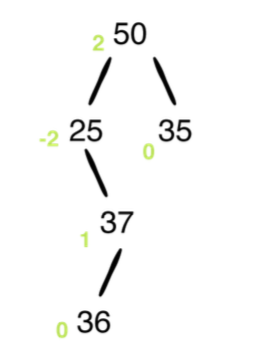
이 경우 왼쪽 회전을하면 트리가 균형을 이루지 않습니다. 이와 같은 경우를 처리하는 방법은 왼쪽 회전을하기 전에 오른쪽 자식에 대해 오른쪽 회전을 수행하는 것입니다. 절차는 다음과 같습니다.

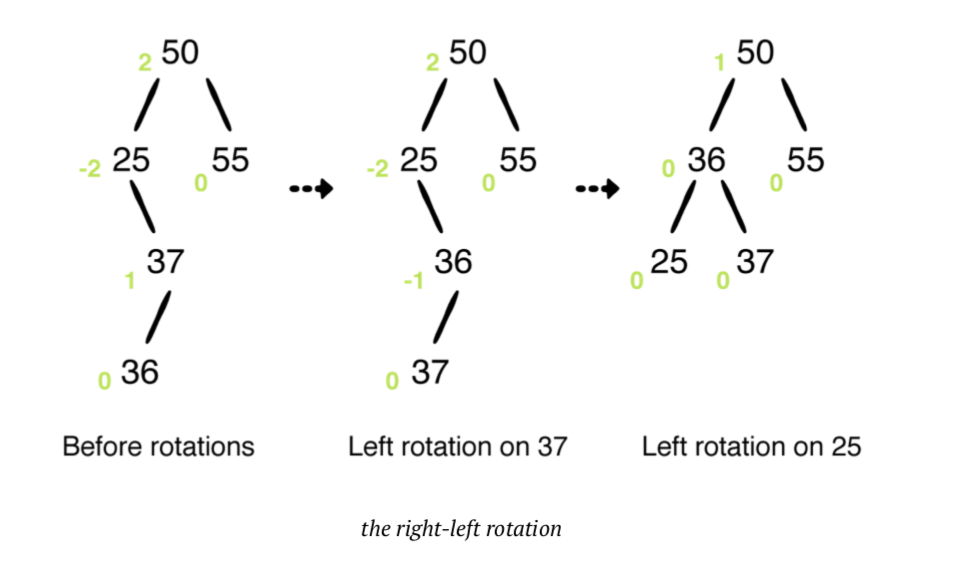
37에 오른쪽 회전을 적용 시킵니다.
이제 노드 25, 36 및 37이 모두 올바른 하위 항목이므로 트리의 균형을 유지하기 위해 왼쪽 회전을 적용할수 있습니다.

/**
 오른쪽 회전후 -> 왼쪽 회전 한 Node를 반환(결과적으로 왼쪽 회전 시키기 위해서 오른쪽 회전을함.)
 */
private func rightLeftRotate(_ node: AVLNode<Element>) -> AVLNode<Element> {
    guard let rightChild = node.rightChild else { return node }
    // 노드의 오른쪽 자식을 오른쪽 회전 시키고,
    node.rightChild = rightRotate(rightChild)
    return leftRotate(node)
}

이것이 언제 호출되는지는 아직 걱정하지말고, 다음을 확인합니다.

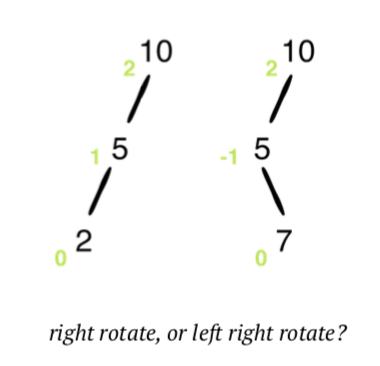
left-right rotation

Left-Right 회전은 Right-Left의 반대 대칼코마니 버전입니다.

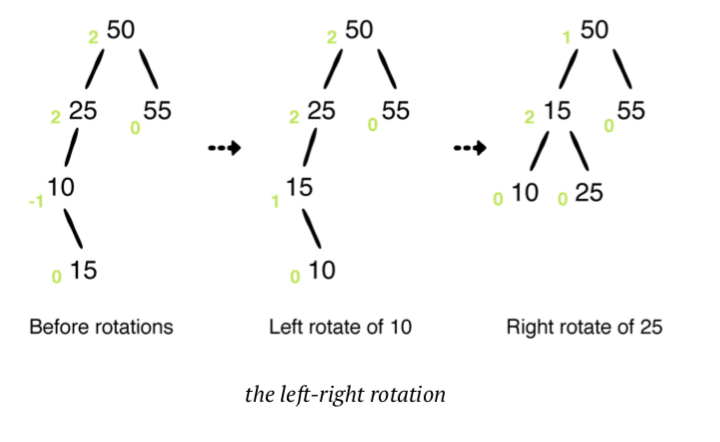
노드 10을 왼쪽 회전 합니다.
노드 25, 15 및 10은 모두 왼쪽 자식이므로 트리의 균형을 조정하기 위해 오른쪽 회전을 적용 할 수 있습니다.

private func leftRightRotate(_ node: AVLNode<Element>) ->
AVLNode<Element> {
  guard let leftChild = node.leftChild else {
return node }
  node.leftChild = leftRotate(leftChild)
  return rightRotate(node)
}

Balance

다음 작업은 balanceFactor를 사용하여 노드 균형 조정이 필요한지 여부를 결정하는 방법을 설계하는 것입니다.

세가지 고려사항이 있습니다.

balanceFactor가 2 이면, 왼쪽 자식이 오른쪽 자식보다 무겁습니다. 이것은 오른쪽, 왼쪽,오른쪽 회전을 사용해야 함을 의미합니다
- 왼쪽이 무거우면 오른쪽 회전, 왼쪽-오른쪽 회전
balanceFactor가 -2 이면, 오른쪽 자식이 왼쪽 자식보다 무겁다는것을 의미합니다. 왼쪽 또는 오른쪽-왼쪽 회전을 사용해야합니다
- 오른쪽이 무거우면 왼쪽, 오른쪽-왼쪽 회전
기본 경우는 특정 노드가 균형을 이룬다느 ㄴ것을 나타냅니다. 노드를 반환하는 것 외에는 여기서 할일이 없습니다.

balanceFactor의 신호를 사용하여 한번 혹은 두번 회전이 필요한지 결정할수 있습니다.

private func balanced(_ node: AVLNode<Element>) -> AVLNode<Element> {
    switch node.balanceFactor {
        // 1
    case 2:
        // 왼쪽-오른쪽 회전을 해야하는 경우
        if let leftChild = node.leftChild, leftChild.balanceFactor == -1 {
            return leftRightRotate(node)
            // 오른쪽 회전만 하는 경우
        }else {
            return rightRotate(node)
        }
        // 2
    case -2:
        if let rightChild = node.rightChild, rightChild.balanceFactor == 1 {
            return rightLeftRotate(node)
        }else {
            return leftRotate(node)
        }
    // 3
    default:
        return node
    }
}

균형은 적절한 처리를 결정하기 위해 balanceFactor을 검사합니다. 남은것은 적절한 지점에서 balance를 호출하는 것입니다.

Revisiting insertion

이미 대부분의 작업을 완료했고, 나머지는 간단합니다

삽입후 직접 노드를 반환하는 대신 균형 잡힌 노드로 전달합니다. 이렇게하면 호출 스택의 모든 노드에서 균형 조정 문제를 검사합니다. 또한 노드의 높이를 업데이트 합니다.

// 1
private func insert(from node: AVLNode<Element>?, value: Element) ->
AVLNode<Element> {
  guard let node = node else {
    return AVLNode(value: value)
  }
  if value < node.value {
    node.leftChild = insert(from: node.leftChild, value: value)
} else {
    node.rightChild = insert(from: node.rightChild, value: value)
  }
  let balancedNode = balanced(node)
  balancedNode.height = max(balancedNode.leftHeight,
balancedNode.rightHeight) + 1
  return balancedNode
}

// 2
example(of: "repeated insertions in sequence") {
  var tree = AVLTree<Int>()
  for i in 0..<15 {
    tree.insert(i)
  }
  print(tree)
}

Revisiting Remove

AVLTree에서 Remove의 마지막 반환값을 삭제하고 아래의 값으로 변경합니다.

let balancedNode = balanced(node)
balancedNode.height = max(balancedNode.leftHeight,
balancedNode.rightHeight) + 1
return balancedNode

Test

example(of: "removing a value") {
  var tree = AVLTree<Int>()
  tree.insert(15)
  tree.insert(10)
  tree.insert(16)
  tree.insert(18)
  print(tree)
  tree.remove(10)
  print(tree)
}

전체 코드 주소

더 알아보면 좋은것들

swift-algorithm-club/Red-Black Tree
swift-algorithm-club/Trie
swift-algorithm-club/Radix Tree
swift-algorithm-club/Splay Tree
swift-algorithm-club/B-Tree

Reference

swift-algorithm-club/AVL Tree/
Data Structures and Algorithms in Swift

Swift, Data Structure, AVL Trees

Georgy Adelson-Velsky and Evgenii Landis의 AVL Tree를 만들어보자!

Swift, Data Structure, AVL Trees

Georgy Adelson-Velsky and Evgenii Landis의 AVL Tree를 만들어보자!

Contents

AVL Trees

Understanding balance

Perfect balance

“Good-enough” balance

Unbalanced

Implementation

Mersuring balance

Rotations

Left rotation

Right Rotation

Right-left rotation

left-right rotation

Balance

Revisiting insertion

Revisiting Remove

Test

더 알아보면 좋은것들

Reference