Contents
- Outline of Binary Search Tree
- Case study: Array vs BST
- Lookup
- Insertion
- Removal
- limitation
- Implementation
- Inserting elements
- Finding elements
- Removing elements
- case1: Leaf node
- case2: Nodes with one child
- case 3: Nodes with two children
- Reference
Outline of Binary Search Tree
Binary Search Tree(BST)는 빠른 검색, 데이터 추가 및 제거 작업을 수월하게 해주는 자료 구조 입니다. 각 연산의 평균 시간 복잡도는 O(log n) 입니다. 이는 Array, Linked List와 같은 선형 데이터 구조보다 상당히 빠릅니다.
Binary Search Tree는 두가지 룰이 있습니다
- 왼쪽 자식의 값은 그들의 부모값보다 작아야합니다.
- 오른쪽 자식의 값은 그들의 부모값보다 커야 합니다.
위의 규칙들은 트리가 의사결정 나무 처럼 행동하게 합니다.
Case study: Array vs BST
이진 검색 트리의 성능을 설명하기 위해 몇 가지 일반적인 작업을 살펴보고 배열의 성능을 이진 검색 트리와 비교합니다.
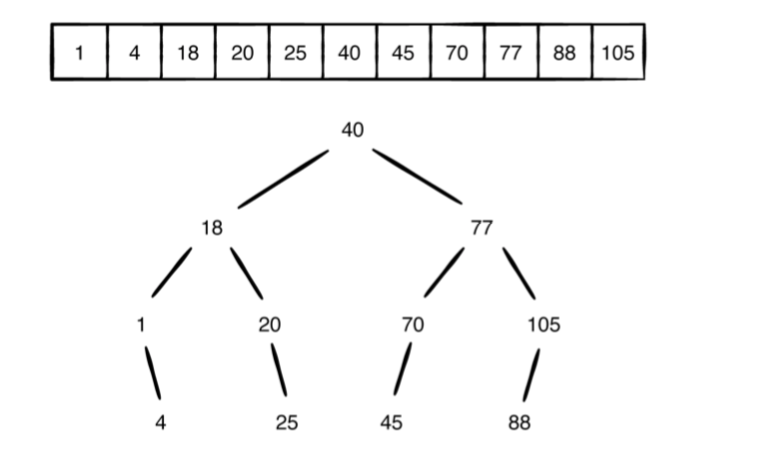
Lookup
정렬되지 않은 배열에서 값을 찾는 방법은 하나뿐입니다. 처음부터 끝까지 각 요소들을 검사하는 것입니다. 따라서 array.contains(:)는 O(n) 입니다.
이진 검색 트리는 큰값과 작은 값을 비교하며 값을 찾아갑니다. 따라서 BST에서 각 요소의 조회가 O(log n)인 이유입니다.
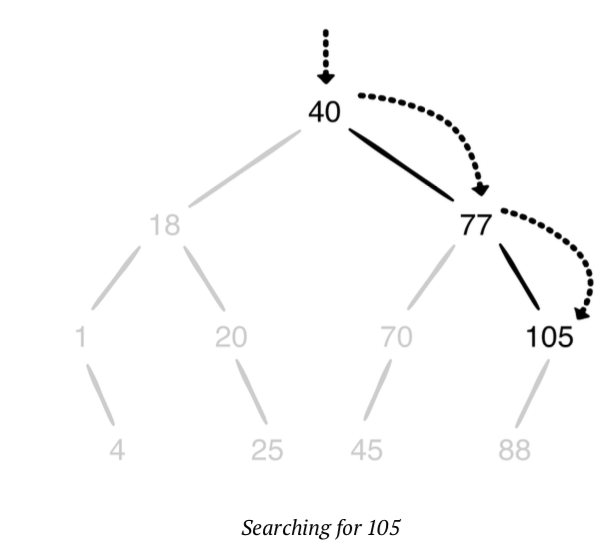
Insertion
삽입 작업의 성능도 비슷한 이야기를 따릅니다.
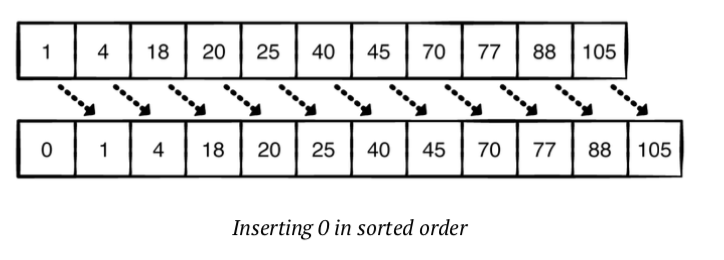
위의 예에서는 0이 배열 앞에 삽입되어 다른 모든 요소가 한 위치만큼 뒤로 이동 합니다. 배열에 값을 삽입하는 것은 O(n)의 시간 복잡도를 가집니다.
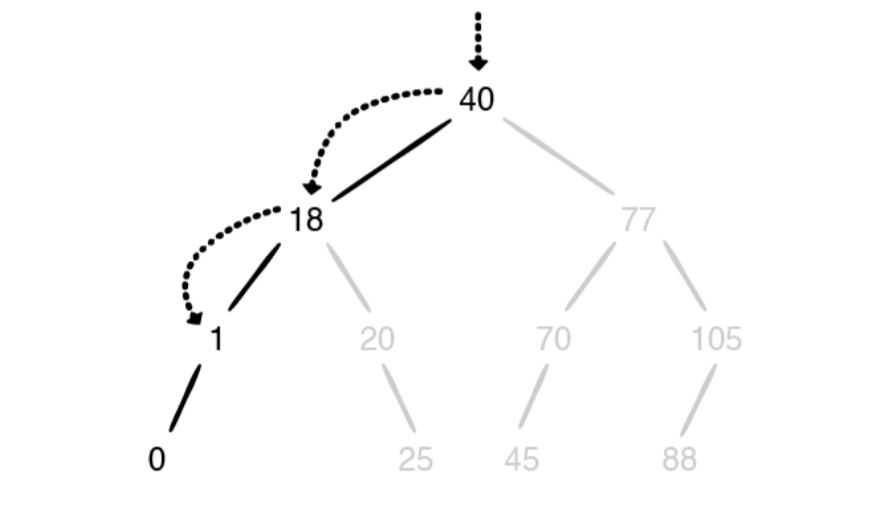
BST에 대한 규칙을 활용하면 삽입 위치를 찾기 위해 세 번의 탐색 만 수행하면되며 주변의 모든 요소를 뒤섞어 쓸 필요가 없습니다! BST에 요소를 삽입하는 작업은 O(log n) 입니다.
Removal
삽입과 마찬가지로, 배열에서 요소를 제거하면 요소가 각 요소들이 이동합니다.
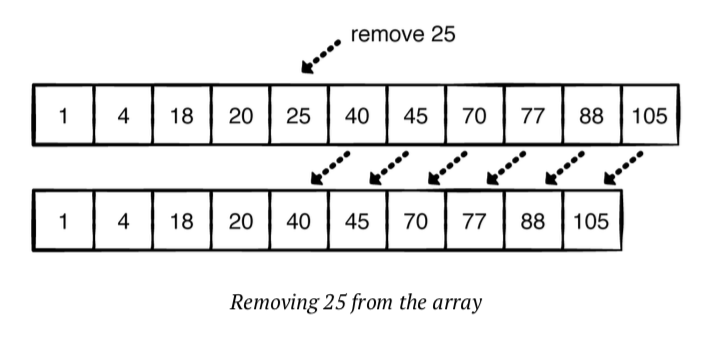
다음은 BST에서 삭제입니다.
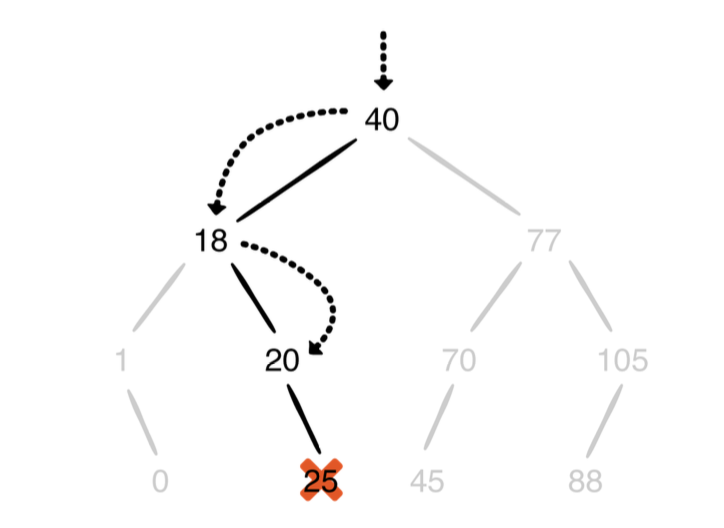
제거할 노드의 자식 유무에 따라서 구현의 복잡성이 다르겠지만 BST에서 요소를 제거 하는 것은 여전히 O(log n) 입니다. 이진 검색 트리를 사용하면 추가, 제거 및 검색 작업의 횟수가 크게 줄어 듭니다.
limitation
이진 검색 트리의 한계점은 자료의 구성이 정렬된 상태로 있어야합니다. 이진 검색 트리의 장점인 추가, 제거 및 검색의 성능은 O(Log h) 입니다.
Implementation
// helper
public class BinaryNode<Element> {
public var value: Element
public var leftChild: BinaryNode?
public var rightChild: BinaryNode?
public init(value: Element) {
self.value = value
}
}
extension BinaryNode: CustomStringConvertible {
public var description: String {
return diagram(for: self)
}
private func diagram(for node: BinaryNode?,
_ top: String = "",
_ root: String = "",
_ bottom: String = "") -> String {
guard let node = node else {
return root + "nil\n"
}
if node.leftChild == nil && node.rightChild == nil {
return root + "\(node.value)\n"
}
return diagram(for: node.rightChild, top + " ", top + "┌──", top + "│ ")
+ root + "\(node.value)\n"
+ diagram(for: node.leftChild, bottom + "│ ", bottom + "└──", bottom + " ")
}
}
extension BinaryNode {
public func traverseInOrder(visit: (Element) -> Void) {
leftChild?.traverseInOrder(visit: visit)
visit(value)
rightChild?.traverseInOrder(visit: visit)
}
public func traversePreOrder(visit: (Element) -> Void) {
visit(value)
leftChild?.traversePreOrder(visit: visit)
rightChild?.traversePreOrder(visit: visit)
}
public func traversePostOrder(visit: (Element) -> Void) {
leftChild?.traversePostOrder(visit: visit)
rightChild?.traversePostOrder(visit: visit)
visit(value)
}
}
// 1
public struct BinarySearchTree<Element: Comparable> {
public private(set) var root: BinaryNode<Element>?
public init() {}
}
// 2
extension BinarySearchTree: CustomStringConvertible {
public var description: String {
return root?.description ?? "empty tree"
}
}
정의에 따라서 이진 검색 트리는 Comparable을 체택한 값만 가질수 있습니다.
Inserting elements
BST규칙에 따라서 왼쪽 자식 노드에는 현재 노드보다 작은 값이 있어야 합니다. 오른쪽 자식 노드는 현재의 값보다 크거나 같은 값이 있어야 합니다.
extension BinarySearchTree {
/**
해당 함수는 사용자 인터페이스로 공개되는 함수이고, 내부적으로는 다른 함수의 재귀적인 실행에 의해서 값이 추가 됩니다.
*/
public mutating func insert(_ value: Element) {
root = insert(from: root, value: value)
}
private mutating func insert(from node: BinaryNode<Element>?, value: Element) -> BinaryNode<Element> {
// root에 값이 없는 경우에 값을 추가한 경우에는 root의 값을 추가한다.
// 혹은 아래의 if, else 구문에서 left,right 자식 노드에 추가될때 호출됨.
guard let node = node else { return BinaryNode<Element>(value: value)}
// 추가한 값이, 해당 node의 값보다 작으면 해당 노드의 왼쪽 자식 노드에
if value < node.value {
node.leftChild = insert(from: node.leftChild, value: value)
} else {
node.rightChild = insert(from: node.rightChild, value: value)
}
return node
}
- 재귀적인 메소드 이므로 재귀를 종결하기 위한 조건이 필요합니다. 현재 노드가 nil이면 삽입점을 찾은것
- 새 값이 현재 값보다 작으면 왼쪽 자식 노드에서 insert를 호출합니다. 새 값이 현재 값보다 크거나 같으면 오른쪽 자식 노드에서 insert를 호출합니다
// 2
example(of: "building a BST") {
var bst = BinarySearchTree<Int>()
for i in 0..<5 {
bst.insert(i)
}
print(bst)
}
아래 이미지의 트리는 불균형해보이지만, BST의 규칙을 따릅니다. 그러나 이 트리 레이아웃은 바람직하지 않은 결과를 가지고 있습니다.
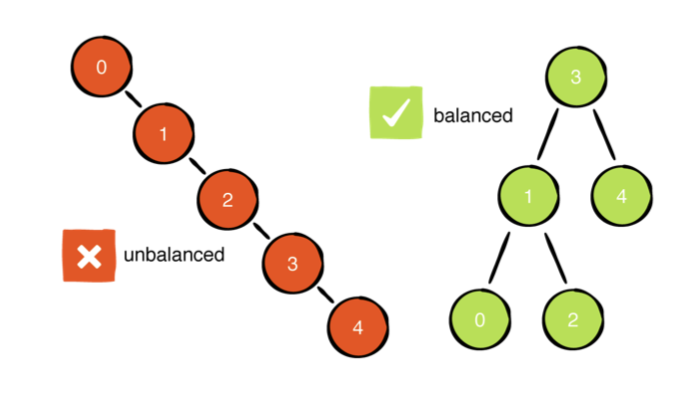
불균형 트리는 성능에 영향을 줍니다. 불균형 트리에 추가로 5를 삽입하면 연산은 O(n) 연산이 됩니다.
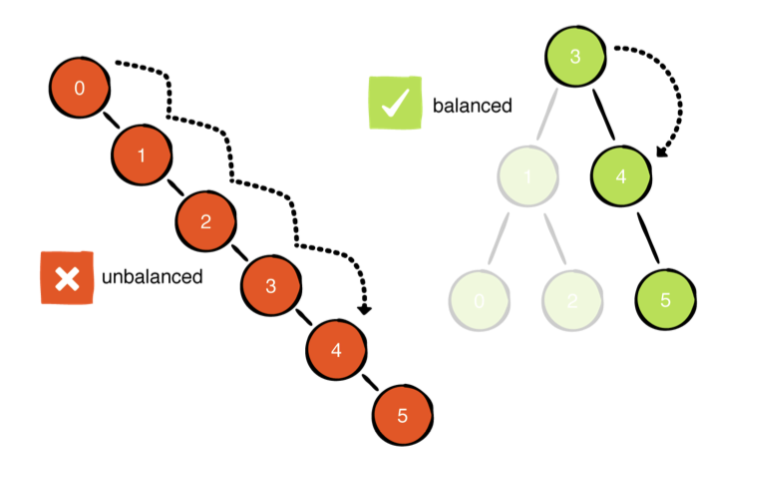
똑똑한 기법을 사용하여 균형 잡힌 구조를 유지하는 자체균형 트리의 구조를 만들 수 있지만. 여기서는 다루지 않습니다.
Finding elements
// 1
public func contains(_ value: Element) -> Bool {
// 1
var current = root
// 2
while let node = current {
// 3
if node.value == value {
return true
}
// 4
if value < node.value {
current = node.leftChild
} else {
current = node.rightChild
}
}
return false
}
// 2
example(of: "finding a node") {
if exampleTree.contains(5) {
print("Found 5!")
} else {
print("Couldn't find 5")
}
}
traversal 을 통해서 모든 요소와 하나씩 비교하지 않고, root을 기준으로 각 값을 비교하며 찾아 갑니다.
Removing elements
이진 검색 트리의 요소를 지우는 방법에는 여러가지 시나리오들이 있습니다.
case1: Leaf node
Leaf node가 삭제해야할 대상일때는 해당 대상을 찾고, 분리 하는 것만으로도 충분합니다.
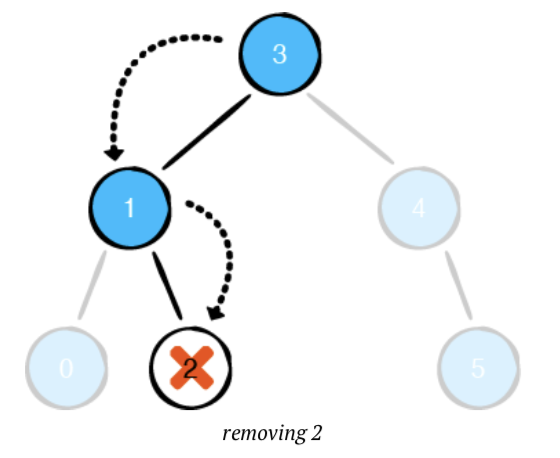
case2: Nodes with one child
하나의 자식 노드를 가진 노드를 지울때는 남겨진 하나의 자식 노드를 지우려고 하는 노드의 부모 노드와 재연결 하는 작업이 필요합니다.
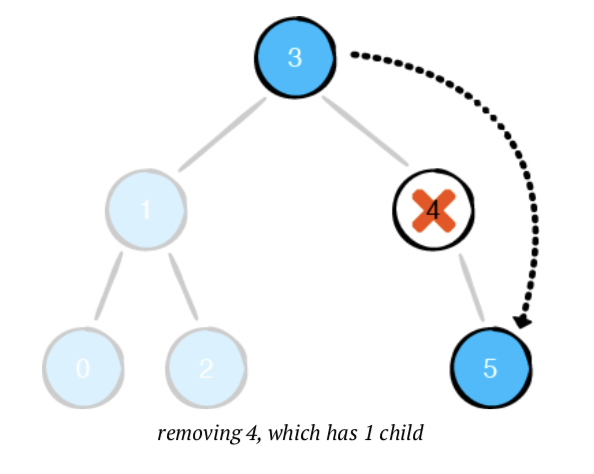
case 3: Nodes with two children
두개의 자식 노드를 가지고 있는 노드를 지울때는 조금 복잡합니다. 아래의 이미지에서 25의 값을 가지고 있는 노드를 지운다고 상상합니다.
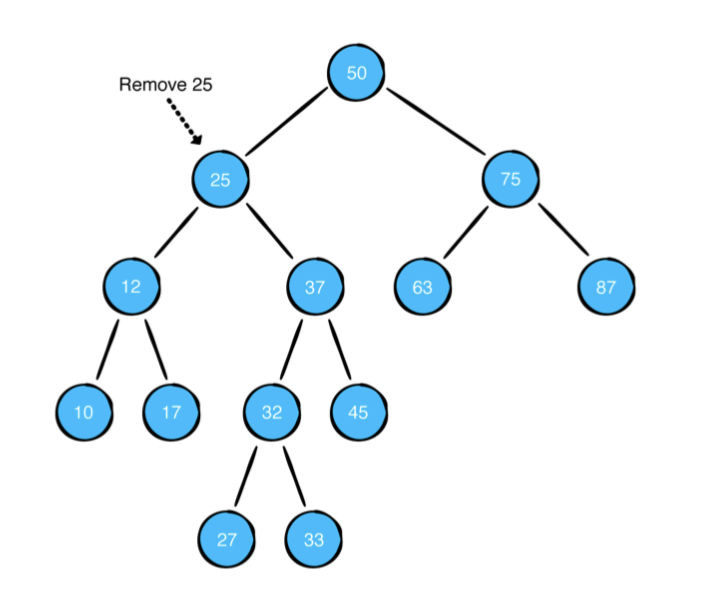
25값을 가진 노드를 지웠을때의 딜레마를 찾아볼수 있습니다.
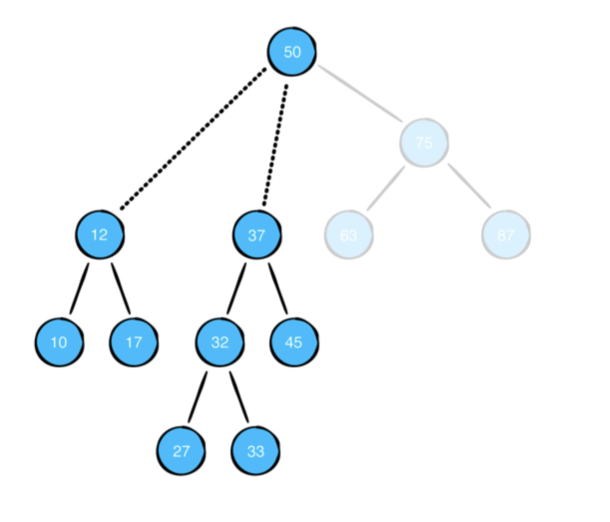
12, 37 값을 가진 자식 노드를 재 연결 해야합니다. 그러나 부모 노드는 최대 두개의 자식 노드를 가질수 있습니다. 이때 지우려고 하는 노드의 오른쪽 서브 트리의 가장 작은 값으로 대체할수 있습니다.
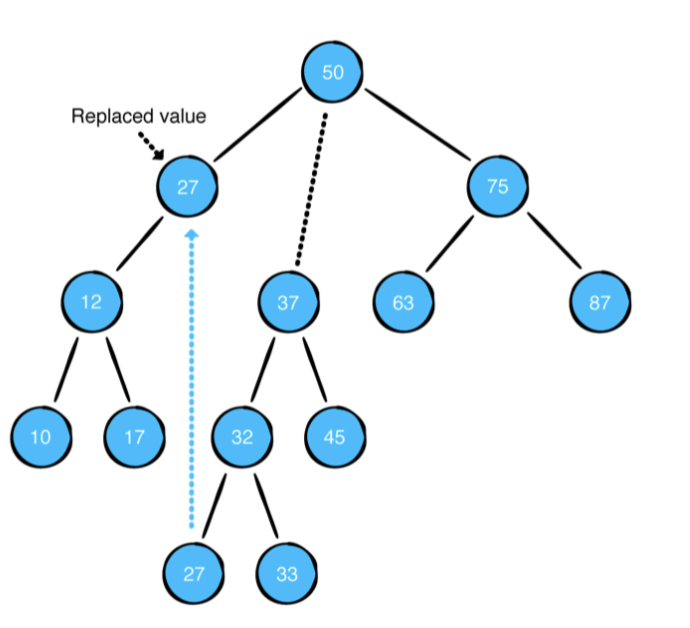
새 노드가 오른쪽 하위 트리에서 왔기 떄문에 왼족 하위 트리의 모든 노드가 새 노드보다 작은 값을 가집니다. 스왑을 수행 한 후에는 단순히 복사한 단말 노드의 값을 제거하면 됩니다.
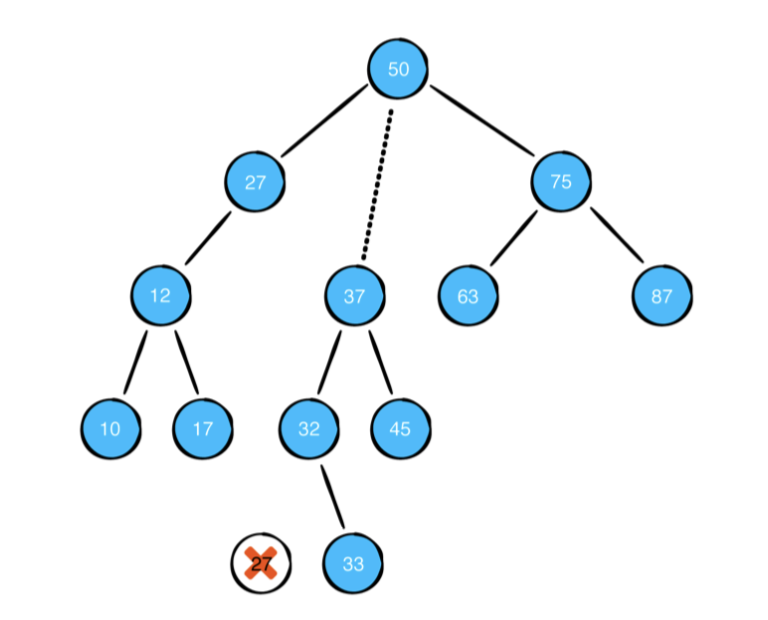
// 1
private extension BinaryNode {
// 재귀적으로 해당 노드를 기준으로 가장 작은값 반환, 만약 nil 이라면, 현재의 자기 자신 노드 반환
var min: BinaryNode {
return leftChild?.min ?? self
}
}
// 2
extension BinarySearchTree {
public mutating func remove(_ value: Element) {
root = remove(node: root, value: value)
}
private mutating func remove(node: BinaryNode<Element>?, value: Element) -> BinaryNode<Element>? {
guard let node = node else { return nil }
/**
1. 지우려고 하는 값이, 현재 node의 값과 같은 경우
- 여기에서 지울수 있는 케이스가 3가지가 나옴
2. 지우려고 하는 값이, 현재 node의 값보다 작은 경우
- 현재 node의 왼쪽 자식 노드로 remove 재귀적으로 실행
3. 지우려고 하는 값이, 현재 node의 값보다 큰 경우
- 현재 node의 오른쪽 자식 노드로 remove 재귀적으로 실행
*/
if value == node.value {
if node.leftChild == nil && node.rightChild == nil { return nil }
if node.leftChild == nil { return node.rightChild }
if node.rightChild == nil { return node.leftChild }
node.value = node.rightChild!.min.value
node.rightChild = remove(node: node.rightChild, value: node.value)
}else if value < node.value {
node.leftChild = remove(node: node.leftChild, value: value)
}else {
node.rightChild = remove(node: node.rightChild, value: value)
}
return node
}
}
// 3
example(of: "removing a node") {
var tree = exampleTree
print("Tree before removal:")
print(tree)
tree.remove(3)
print("Tree after removing root:")
print(tree)
}
Reference
swift-algorithm-club/Binary Search Tree/
Data Structures and Algorithms in Swift