Contents
- Outline of Binary Tree
- Types and Kinds
- Implementation
- Building a diagram
- Traversal Algorithms
- In-order traversal
- Pre-order traversal
- Post-order traversal
- Reference
Outline of Binary Tree
이진 트리(Binary Tree)는 각 노드가 두개의 자식 노드를 가질수 있습니다. 그리고 그것들을 left, right 자식 처럼 참조합니다.
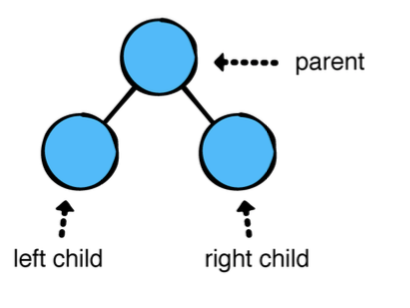
이진 트리는 많은 트리 구조와 알고리즘에 기초 역할을 합니다.
types and kinds
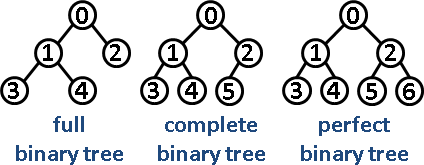
- Full binary tree: 트리 내의 특정 노드 N이 있을 때, N은 0개 혹은 2개의 자식 노드를 지닙니다.(1개의 자식 노드를 지니는 경우는 없습니다.
- Perfect binary tree: 모든 내부 노드는 두 개의 자식 노드를 지니며, 모든 잎은 동일한 깊이를 지닙니다.
- Complete binary tree: 마지막 레벨을 제외한 모든 레벨이 노드로 완전하게 찬 상태입니다. 트리의 좌측 방향으로 뻗어나간 마지막 레벨은 완전하게 채워질 수 없습니다.
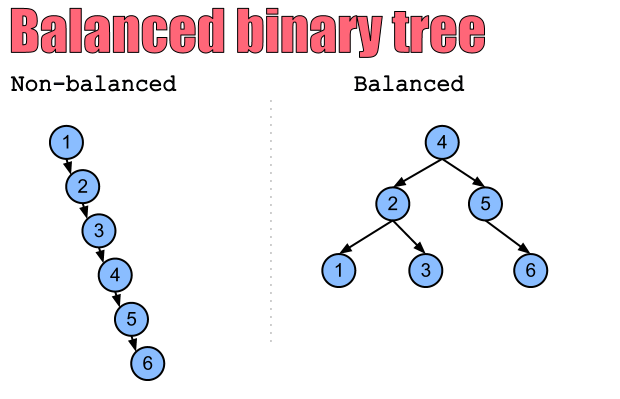
- Balanced binary tree: 잎 노드까지 이어지기 위한 최소한의 높이만을 지닙니다.
Implementation
// helper
public func example(of description: String, action: () -> Void) {
print("---Example of \(description)---")
action()
print()
}
// 1
public class BinaryNode<Element> {
public var value: Element
public var leftChild: BinaryNode?
public var rightChild: BinaryNode?
public init(value: Element) {
self.value = value
}
}
// 2
var tree: BinaryNode<Int> {
let zero = BinaryNode(value: 0)
let one = BinaryNode(value: 1)
let five = BinaryNode(value: 5)
let seven = BinaryNode(value: 7)
let eight = BinaryNode(value: 8)
let nine = BinaryNode(value: 9)
seven.leftChild = one
one.leftChild = zero
one.rightChild = five
seven.rightChild = nine
nine.leftChild = eight
return seven
}
위의 연산 프로퍼티는 아래의 트리를 구조를 반환합니다.
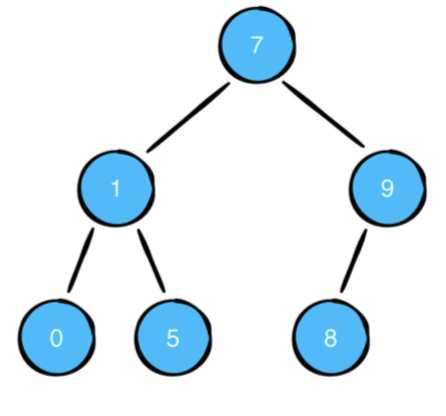
Building a diagram
어떤 경우에는 실제 구조를 눈으로 보는게 유용할수 있습니다. 아래 알고리즘은 Károly Lőrentey에 의해서 구현 되었습니다.
// 1
extension BinaryNode: CustomStringConvertible {
public var description: String {
return diagram(for: self)
}
private func diagram(for node: BinaryNode?,
_ top: String = "",
_ root: String = "",
_ bottom: String = "") -> String {
guard let node = node else {
return root + "nil\n"
}
if node.leftChild == nil && node.rightChild == nil {
return root + "\(node.value)\n"
}
return diagram(for: node.rightChild, top + " ", top + "┌──", top + "│ ")
+ root + "\(node.value)\n"
+ diagram(for: node.leftChild, bottom + "│ ", bottom + "└──", bottom + " ")
}
}
}
// 2
example(of: "tree diagram") {
print(tree)
}
// 3
---Example of tree diagram---
┌──nil
┌──9
│ └──8
7
│ ┌──5
└──1
└──0
Traversal Algorithms
이진 트리에 대한 전위 순회(Pre-order traversal), 중위 순회(In-order traversal) 및 후위 순회(post-order traversal)의 세 가지 탐색 알고리즘을 살펴 보겠습니다.
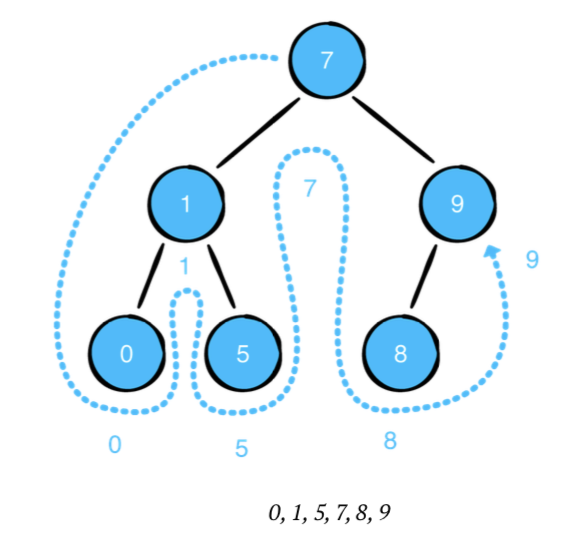
In-order traversal
- 현재 노드가 왼쪽 자식이 있다면 재귀적으로 자식 노드를 먼저 방문합니다.
- 그후 자식노드 그 자신을 방문합니다
- 현재 노드가 오른쪽 자식을 가졌다면 재귀적으로 그 자식노드를 방문합니다.
좌측 값 -> 루트 노드 값 -> 우측 값
// 1
public func traverseInOrder(visit: (Element) -> Void) {
leftChild?.traverseInOrder(visit: visit)
visit(value)
rightChild?.traverseInOrder(visit: visit)
}
// 2
example(of: "in-order traversal") {
tree.traverseInOrder { print($0) }
}
// 3
---Example of in-order traversal---
0
1
5
7
8
9
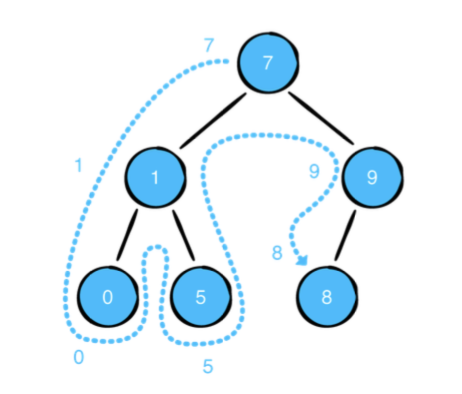
Pre-order traversal
전위 순회는 항상 현재의 노드를 먼저 방문하고 왼쪽과 오른쪽 자식을 재귀적으로 방문합니다.
// 1
public func traversePreOrder(visit: (Element) -> Void) {
visit(value)
leftChild?.traversePreOrder(visit: visit)
rightChild?.traversePreOrder(visit: visit)
}
// 2
example(of: "pre-order traversal") {
tree.traversePreOrder { print($0) }
}
// 3
---Example of pre-order traversal---
7
1
0
5
9
8
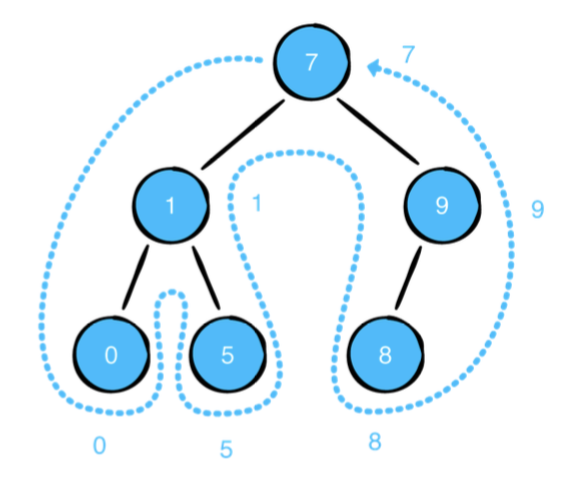
Post-order traversal
후위 순회는 왼쪽과 오른쪽 자식 노드가 모두 재귀적으로 방문된 이후에 현재 노드를 방문합니다.
// 1
public func traversePostOrder(visit: (Element) -> Void) {
leftChild?.traversePostOrder(visit: visit)
rightChild?.traversePostOrder(visit: visit)
visit(value)
}
// 2
example(of: "post-order traversal") {
tree.traversePostOrder { print($0) }
}
// 3
---Example of post-order traversal---
0
5
1
8
9
7
Reference
swift-algorithm-club/Binary Tree/
Data Structures and Algorithms in Swift