Contetns

• Heap Sort
• Getting started
• Implemenetation
• Performence
• Reference

Heap Sort

Heap sort는 Heap을 사용하여 배열을 오름차순으로 정렬하는 또 다른 비교 알고리즘 입니다. Heap Sort는 다음과 같은 특성을 가진 부분적으로 정렬된 이진 트리 인 힙을 사용합니다

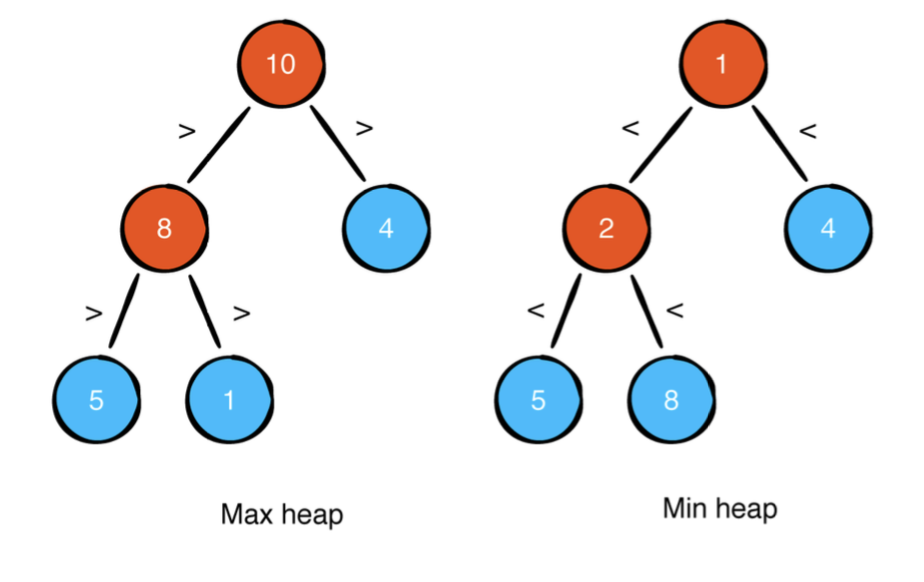
1. 최대힙에서는 모든 부모 노드가 자식 노드보다 큰 값을 가진 가집니다
2. 최소힙에서는 모든 상위 노드가 하위 노드보다 작은 값을 가진 집니다

Getting started

정렬되지 않은 배열의 경우, 가장 낮은 값에서 가장 큰 값으로 정렬하려면 먼저 이 배열을 최대 힙으로 변환해야합니다.

이 변환은 모든 부모 노드가 올바른 위치에 있도록 선별하여 수행됩니다. 결과로 나오는 최대 힙은 다음과 같습니다.

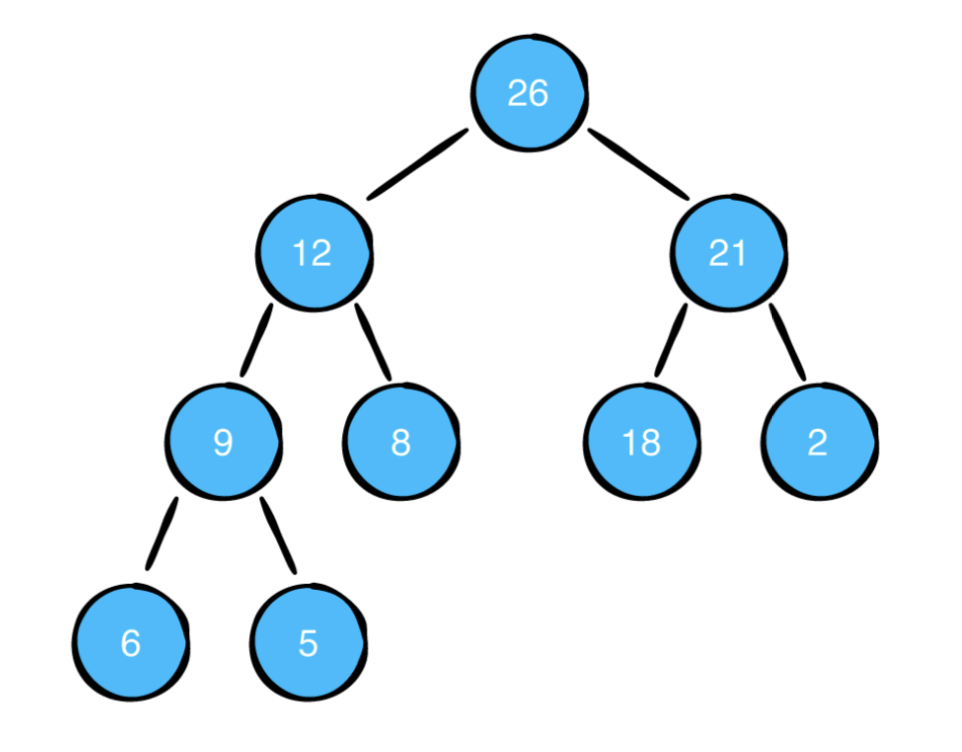
이것은 다음 과같이 보여집니다.

단일 선별 작업의 시간 복잡성은 O(log n)이기 때문에 힙을 작성하는 데 소요되는 총 시간은 O(n log n)입니다.

이제 이 배열을 어떻게 오름차순으로 정렬하는지 지켜봅니다.

최대힙에서는 항상 가장큰 값을 가진 요소가 루트 노드 이기때문에, 첫번째 인덱스 0 과 마지막 인덱스 n-1의 요소를 스왑하는 걸로 시작합니다. 스왑의 결과로 배열의 마지막 값은 올바른 값이 되지만 힙 데이터 구조는 더이상 유효하지 않습니다.

따라서 올바른 다음단계는 sifw down을 통해서 5값을 원래 자리에 도달하게 하는것입니다.

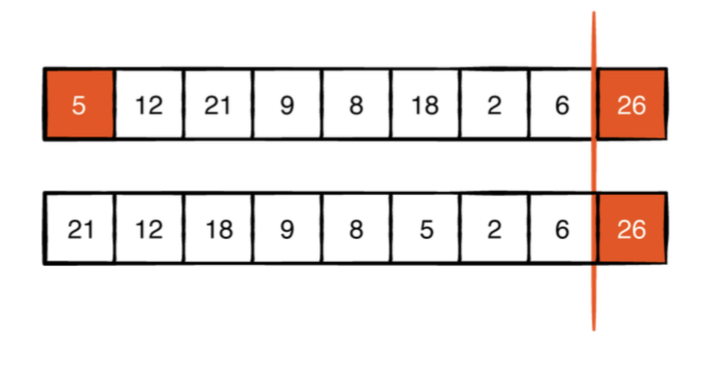
힙의 마지막 요소를 더 이상 힙의 일부가 아니라 정렬 된 배열의 요소로 간주하지 않기 때문에 힙의 마지막 요소를 제외합니다.

5를 이동하면 두 번째로 큰 요소 21이 새로운 루트 요소가 됩니다. 이제 이전 단계를 반복하고 21을 마지막 요소 6으로 바꾸고 힙을 축소 한 다음 6을 아래로 내립니다.

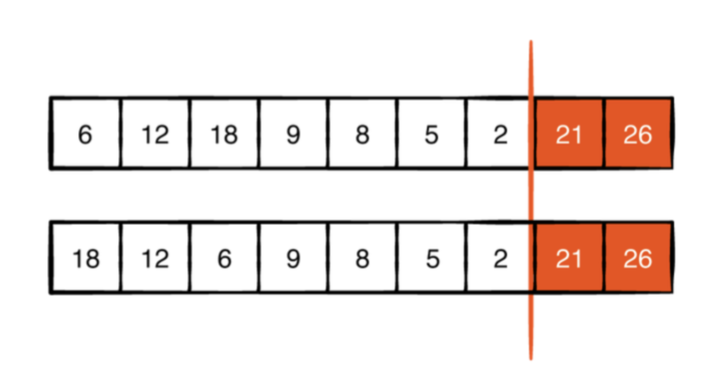
패턴을보기 시작 했나요? 힙 정렬은 매우 간단합니다. 첫 번째 요소와 마지막 요소를 바꿀 때 더 큰 요소가 올바른 순서로 배열의 뒷면으로 나아갑니다. 크기 1의 힙에 도달 할 때까지 스왑 및 선별 단계를 반복하면됩니다. 배열이 완전히 정렬됩니다.

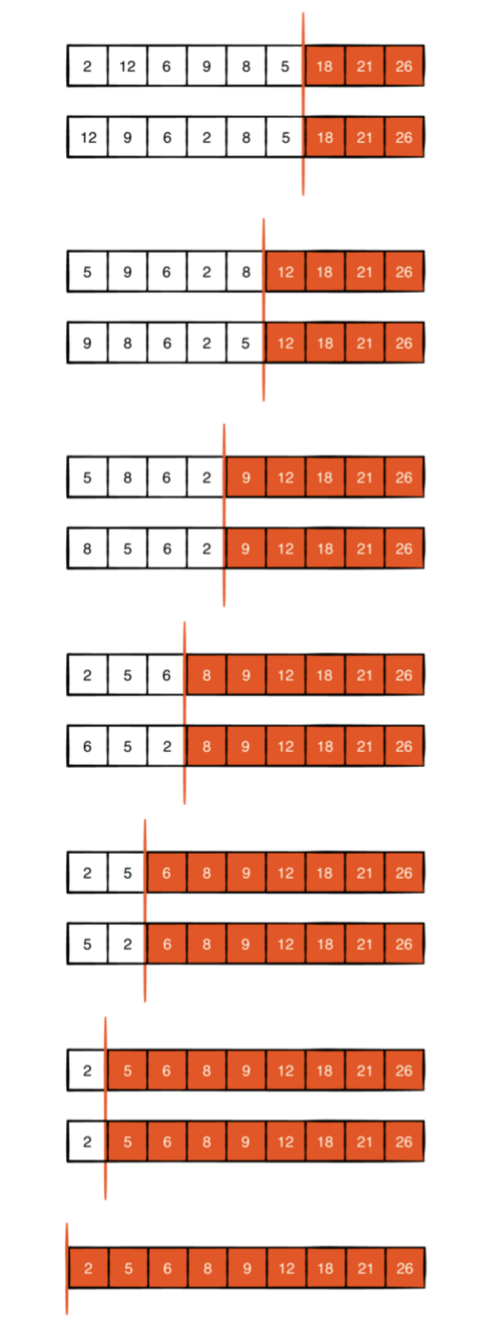
Note: Heap sort의 처리는 selection sort와 비슷합니다.

Implementation

그런 다음 이 정렬 알고리즘을 구현합니다.

extension Heap {
  func sorted() -> [Element] {
    var heap = Heap(sort: sort, elements: elements) // 1
    for index in heap.elements.indices.reversed() { // 2
      heap.elements.swapAt(0, index) // 3
      heap.siftDown(from: 0, upTo: index) // 4
    }
    return heap.elements
  }
}

다음은 진행 상황입니다.

1. 먼저 힙의 복사본을 만듭니다. 힙 정렬이 요소 배열을 정렬 한 후에는 더 이상 유효한 힙이 아닙니다. 힙 사본을 작성하면 힙이 유효한지 확인할 수 있습니다.
2. 마지막 요소에서부터 배열을 반복합니다.
3. 첫 번째 요소와 마지막 요소를 교체합니다. 가장 큰 정렬되지 않은 요소가 올바른 위치로 이동합니다.
4. 힙이 유효하지 않으므로 새 루트 노드를 내려야합니다. 결과적으로 다음으로 큰 요소가 새로운 루트가됩니다.

힙 정렬을 지원하려면 siftDown 메소드에 추가 매개 변수 upTo를 추가해야합니다. 이 방법으로, sift down은 배열의 정렬되지 않은 부분만을 사용하며, 루프의 반복마다 축소됩니다.

let heap = Heap(sort: >, elements: [6, 12, 2, 26, 8, 18, 21, 9, 5])
print(heap.sorted())

Performence

메모리 내 정렬의 이점을 얻지만 힙 정렬의 성능은 최상, 최악 및 평균의 경우 O(nlog n)입니다. 이는 전체 목록을 한 번 순회해야 하기 때문에 요소를 교체 할 때마다 O(log n) 작업 인 화면 이동을 수행해야합니다.

힙 정렬은 요소가 배치되고 힙에 배치되는 방식에 따라 다르므로 안정된 정렬이 아닙니다.

전체 코드 주소

Reference

swift-algorithm-club/Heap
Data Structures and Algorithms in Swift