Note: <혼자 공부하는 머신러닝+딥러닝>을 참고 했습니다.
주성분 분석, 차원과 차원축소에 대해 알아봅니다.
차원과 차원 축소
과일 사진의 경우 10,000개의 픽셀이 있기 떄문에 10,000개의 특성이 있습니다.
머신러닝에서는 이런 특성을 차원(demension) 이라고도 부릅니다.
Note: 2차원 배열과 1차원 배열(벡터)에서는 차원이란 용어는 조금 다르게 사용합니다. 다차원 배열에서 차원은 배열의 축 개수가 됩니다. 가령 2차원 배열일 때는 행과 열의 차원이 되죠. 하지만 1차원 배열, 즉 벡터일 경우에는 원소의 개수를 말합니다.
특성이 많으면 선형 모델의 성능이 높아지고 훈련 데이터에 쉽게 과대적합된다고 알고 있습니다.
차원 축소는 데이터를 가장 잘 나타내는 일부 특성을 선택하여 데이터 크기를 줄이고 지도학습 모델의 성능을 향상시킬 수 있는 방법입니다.
또한 줄어든 차원에서 다시 원본 차원으로 손실을 최대한 줄이면서 복원할 수도 있습니다.
대표적인 차원 축소 알고리즘인 주성분 분석(principal component analysis) 에 대해서 알아 봅니다
주성분 분석(PCA, principal component analysis)
주성분 분석은 데이터에 있는 분산이 큰 방향을 찾는 것으로 이해할 수 있습니다. 분산은 데이터가 널리 퍼져있는 정도를 말합니다. 분산이 큰 방향이란 데이터를 잘 표현하는 어떤 벡터라고 생각할 수 있습니다.
Note: 주성분은 원본 차원과 같고 주성분으로 바꾼 데이터는 차원이 줄어든다는 점을 꼭 기억하세요.
더 자세히 알고 싶다면 여기를 참고하세요.
1
2
3
4
5
6
7
from sklearn.decomposition import PCA
pca = PCA(n_components=50)
pca.fit(fruits_2d)
print(pca.components_.shape)
---
(50, 10000)
n_components=50 으로 지정했기 때문에 pca.components_의 첫번째 차원이 50 입니다. 즉 50개의 주성분을 찾은거죠.
두 번째 차원은 항상 원본 데이터의 특성 개수와 같은 10,000 입니다.
draw_fruits(pca.components_.reshape(-1, 100, 100))
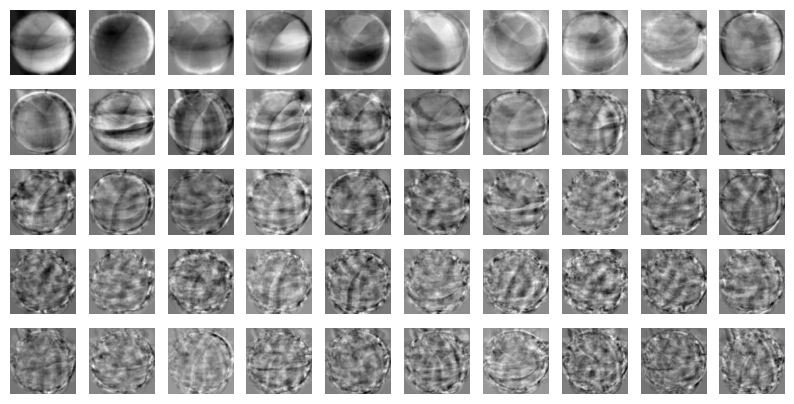
이 주성분은 원본 데이터에서 가장 분산이 큰 방향을 순서대로 나타낸 것입니다. 한편으로는 데이터 셋에 있는 어떤 특징을 잡아낸 것처럼 생각할 수도 있습니다.
주성분을 찾았으므로 원본 데이터를 주성분에 투영하여 특성의 개수를 10,000개에서 50개개로 줄일 수 있습니다. 이는 마치 원본 데이터를 각 주성분으로 분해하는 것으로 생각할 수 있습니다.
print(fruits_2d.shape)
---
(300, 10000)
---
fruits_pca = pca.transform(fruits_2d)
print(fruits_pca.shape)
---
(300, 50)
fruits_2d는 (300, 10000) 크기의 배열 이었습니다. 50개의 주성분을 찾은 PCA모델을 사용해 이를 (300, 50)크기의 배열로 변환했ㅅ브니다.
원본 데이터 재구성
fruits_inverse = pca.inverse_transform(fruits_pca)
print(fruits_inverse.shape)
fruits_reconstruct = fruits_inverse.reshape(-1, 100, 100)
for start in [0, 100, 200]:
draw_fruits(fruits_reconstruct[start:start+100])
print("\n")
 |
 |
 |
일부 흐리고 번진 부분이 있지만 거의 모든 과일이 잘 복원되었습니다. 만약 주성분을 최대로 사용했다면 완벽하게 원본 데이터를 재구성할 수 있을 것 입니다. 그럼 50개의 특성은 얼마나 분산을 보존하고 있는 것일까요?
설명된 분산(explained variance)
주성분이 원본 데이터의 분산을 얼마나 잘 나타내는지 기록한 값을 설명된 분산(explained variance) 라고 합니다.
PCA 크래스의 explained_variance_ratio_에 각 주성분의 설명된 분산 비율이 기록되어 있습니다.
당연히 첫번째 줏어분의 설명된 분산이 가장 큽니다.
이 분산 비율을 모두 더하면 50개의 주성분으로 표현하고 잇는 총 분산 비율을 얻을 수 있습니다.
print(np.sum(pca.explained_variance_ratio_))
---
0.9215533769019285
92%가 넘는 분산을 유지하고 있습니다. 50개의 특성에서 원본 데이터를 복원했을 때 원본 이미지의 품질이 높았던 이유를 여기에서 찾을 수 있습니다.