Note: <혼자 공부하는 머신러닝+딥러닝>을 참고 했습니다.
다중 회귀
여전히 훈련 세트보다 테스트 세트의 점수가 높습니다. 이 문제를 해결하려면 제곱보다 더 고차항을 넣어야 하는데, 얼만큼의 더 고차항을 넣어야 할까요?
Note: “선형 회귀는 특성이 많을수록 효과가 좋다”
여러개의 특성을 사용한 선형 회귀를 다중회귀(multiple regression)라고 부릅니다.
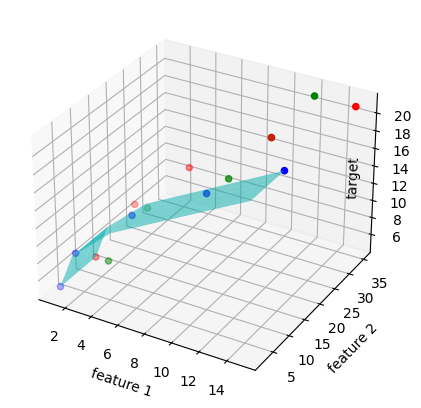
특성이 2개면 타깃값과 함께 3차원 공간을 형성 합니다.
선형 회귀 방정식은 타깃 = a * 특성1 + b * 특성2 * + 절편은 평면이 됩니다.
특성이 3, 4, .. 늘어나는 경우엔 어떻게 될까요? 3차원 공간 이상을 그리거나 상상할 수 없지만, 분명한 것은 선형 회귀를 단순한 직선이나 평면으로 생각하여 성능이 무조건 낮다고 오해해서는 안됩니다.
기존에 갖고있는 특성을 사용해 새로운 특성을 뽑아내는 작업을 특성 공학(feature engineering)라고 부릅니다.
다중 회귀 데이터 준비
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import pandas as pd
import numpy as np
df = pd.read_csv('https://bit.ly/perch_csv_data')
perch_full = df.to_numpy()
perch_weight = np.array(
[5.9, 32.0, 40.0, 51.5, 70.0, 100.0, 78.0, 80.0, 85.0, 85.0,
110.0, 115.0, 125.0, 130.0, 120.0, 120.0, 130.0, 135.0, 110.0,
130.0, 150.0, 145.0, 150.0, 170.0, 225.0, 145.0, 188.0, 180.0,
197.0, 218.0, 300.0, 260.0, 265.0, 250.0, 250.0, 300.0, 320.0,
514.0, 556.0, 840.0, 685.0, 700.0, 700.0, 690.0, 900.0, 650.0,
820.0, 850.0, 900.0, 1015.0, 820.0, 1100.0, 1000.0, 1100.0,
1000.0, 1000.0]
)
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(perch_full, perch_weight, random_state=42)
사이킷런의 변환기
특성을 만들거나 전처리하기 위한 다양한 클래스를 제공합니다. 이런 클래스를 transformer라고 부릅니다..
PolynominalFeatures 클래스는 기본적으로 각 특성을 제곱한 항을 추가하고 특성끼리 서로 곱한 항을 추가합니다.
1
2
3
4
5
6
7
8
9
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(include_bias=False)
poly.fit(train_input)
train_poly = poly.transform(train_input)
print(train_poly.shape)
print(poly.get_feature_names_out())
> (42, 9)
> ['x0' 'x1' 'x2' 'x0^2' 'x0 x1' 'x0 x2' 'x1^2' 'x1 x2' 'x2^2']
출력 결과의 x0은 첫번째 특성을 의미하고 x02는 첫 번째 특성의 제곱을 나타내는 식 입니다.
다중 회귀 모델 훈련하기
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(train_poly, train_target)
print(lr.score(train_poly, train_target))
print(lr.score(test_poly, test_target))
poly = PolynomialFeatures(degree=5, include_bias=False)
poly.fit(train_input)
train_poly = poly.transform(train_input)
test_poly = poly.transform(test_input)
lr.fit(train_poly, train_target)
print(lr.score(train_poly, train_target))
> 0.9999999999989608
> -144.4049046409093
> 0.9999999999989608
특성의 개수를 크게 늘리면 선형 모델은 강력해집니다. 훈련 세트에 대해 거의 완벽하게 학습할 수 있습니다. 하지만 이런 모델은 훈련 세트에 너무 과대적합되므로 테스트 세트에서는 형편없는 점수를 만듭니다.
규제(regularization)
규제는 머신러닝 모델이 훈련 세트를 너무 과도하게 학습하지 못하도록 훼방하는 것을 말합니다. 즉 모델이 훈련 세트에 과대적합되지 않도록 만드는 것이죠. 선형 회귀 모델의 경우 특성에 곱해지는 계수(또는 기울기)의 크기를 작게 만듭니다.
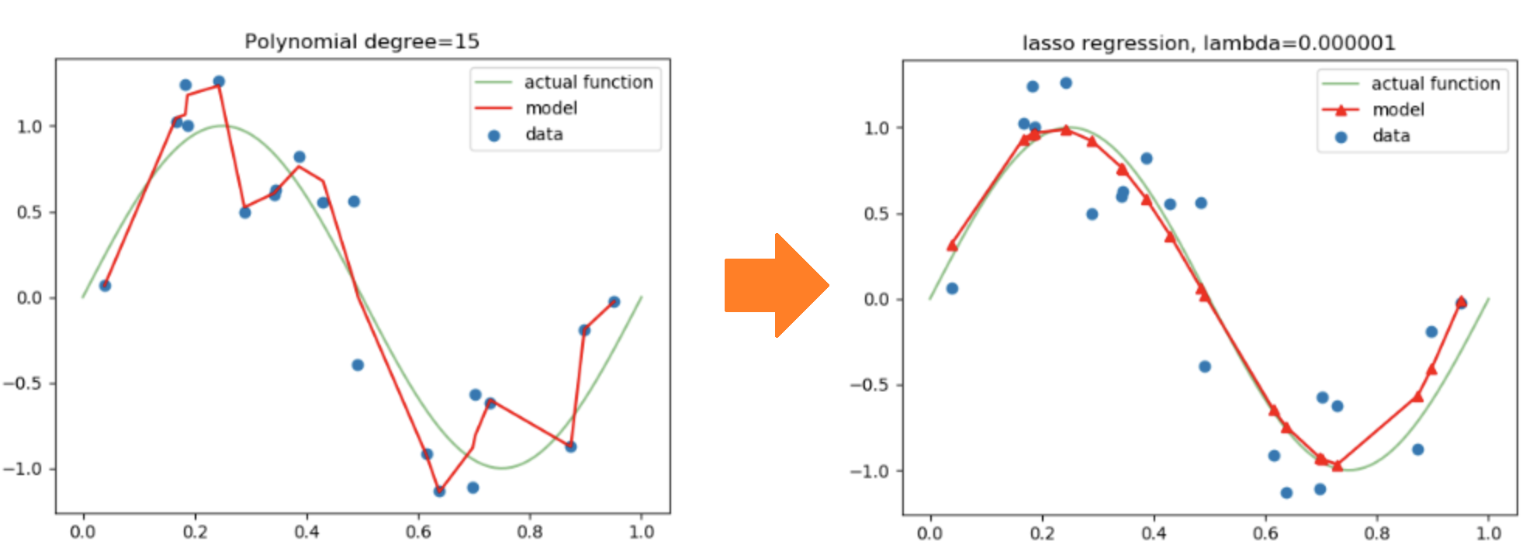
Note: source
선형 회귀 모델에 규제를 적용할때 계수 값의 크기가 서로 많이 다르면 공정하게 제어되지 않습니다. 따라서 규제를 적용하기 전에 정규화를 해야합니다.
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
ss.fit(train_poly)
train_scaled = ss.transform(train_poly)
test_scaled = ss.transform(test_poly)
릿지(ridge) 회귀와 라쏘(lasso 회귀)
선형 회귀 모델에 규제를 추가한 모델을 릿지(ridge) 와 라쏘(lasso)라고 부릅니다. 릿지는 계수를 제곱한 값을 기준으로 규제를 적용하고, 라쏘는 계수의 절대값을 기준으로 규제를 적용합니다.
두 알고리즘 모두 계수의 크기를 줄이지만 라쏘는 아예 0으로 만들 수도 있습니다.
from sklearn.linear_model import Ridge
ridge = Ridge()
ridge.fit(train_scaled, train_target)
print(ridge.score(train_scaled, train_target))
print(ridge.score(test_scaled, test_target))
# > 0.9896101671037343
# > 0.9790693977615387
import matplotlib.pyplot as plt
train_score = []
test_score = []
alpha_list = [0.001, 0.01, 0.1, 1, 10, 100]
for alpha in alpha_list:
# 릿지 모델을 만듭니다
ridge = Ridge(alpha=alpha)
# 릿지 모델을 훈련합니다
ridge.fit(train_scaled, train_target)
# 훈련 점수와 테스트 점수를 저장합니다
train_score.append(ridge.score(train_scaled, train_target))
test_score.append(ridge.score(test_scaled, test_target))
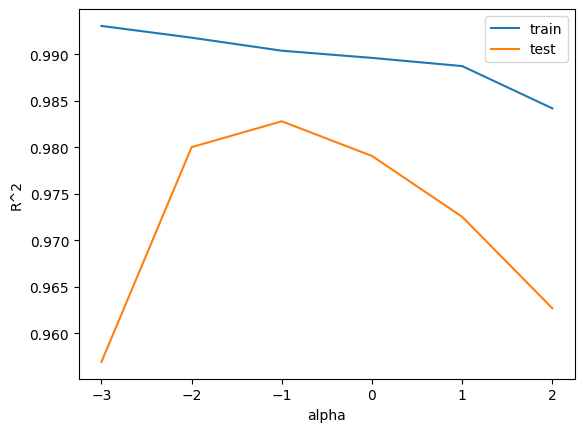
plt.plot(np.log10(alpha_list), train_score)
plt.plot(np.log10(alpha_list), test_score)
plt.xlabel('alpha')
plt.ylabel('R^2')
plt.show()
릿지와 라쏘 모델을 사용할 때 규제의 양을 임의로 조절할 수 있습니다. 모델 객체를 만들 때 alpha매개변수로 규제의 강도를 조절합니다. alpha 값이 크면 규제 강도가 세지므로 계수 값을 더 줄이고 조금 더 과소적합되도록 유도합니다. alpha 값이 작으면 계수를 줄이는 역할이 줄어들고 선형 회귀 모델과 비슷 해지므로 과대적합될 가능성이 큽니다.
적절한 alpha 값을 찾는 한 가지 방법은 alpha 갑ㅅ에 대한 R2값의 그래프를 그려보는 것 입니다.