Note: <혼자 공부하는 머신러닝+딥러닝>을 참고 했습니다.
확률적 경사하강법 SGD(Stochastic Gradient Descent)에 대해서 알아봅니다.
확률적 경사 하강법(Stochastic Gradient Descent)
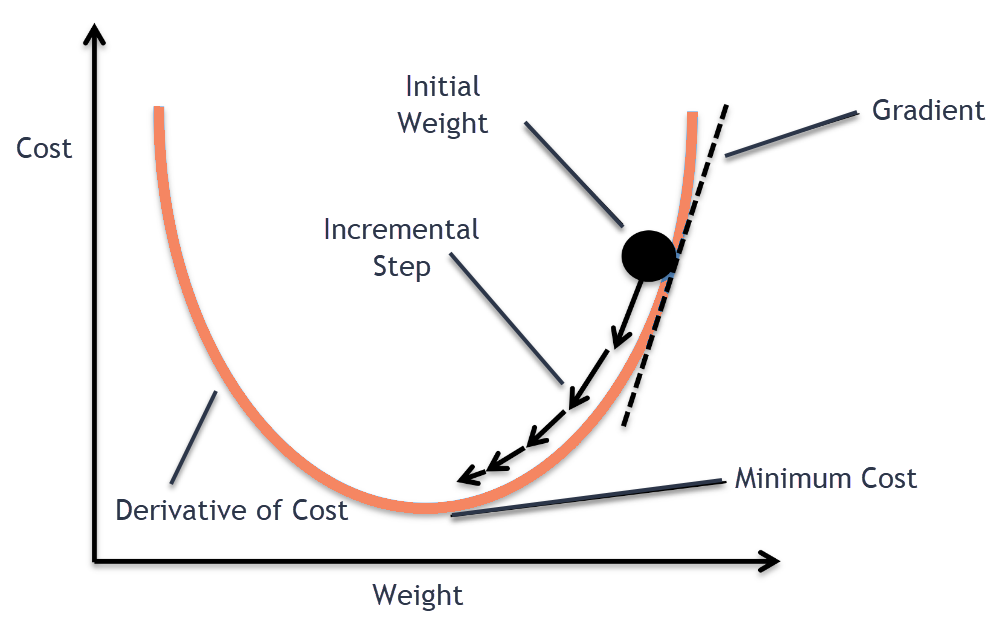
훈련세트에서 랜덤하게 하나의 샘플을 고르는 것이 확률적 경사 하강법 입니다. 확률적 경사 하강법은 훈련 세트에서 랜덤하게 하나의 샘플을 선택하여 가파른 경사를 조금 내려갑니다. 그 다음 훈련 세트에서 랜덤하게 또 다른 샘플을 하나 선택하여 경사를 조금 내려갑니다. 이런 식으로 전체 샘플을 모두 사용할 때까지 계속합니다.
모든 샘플을 다 사용했으면 훈련세트를 다시 채우고 다시 시작합니다. 확률적 경사 하강법에서 훈련 세트를 한 번 모두 사용하는 과정을 에포크(epoch) 라고 합니다.
여러개의 샘플을 사용해 경사 하강법을 수행하는 방식도 있습니다. 미니배치 경사 하강법(minibatch gradient descent)라고 합니다.
또는, 전체 샘플을 사용하는 방법도 있습니다. 배치 경사 하강법(batch gradient descent)라고 부릅니다. 전체 데이터를 상요하기 때문에 가장 안전하지만 컴퓨터 자원을 많이 사용하게 됩니다.
Note: 확률적 경사 하강법을 꼭 사용하는 알고리즘이 있습니다. 바로 신경망 알고리즘 입니다. 신경망은 일반적으로 많은 데이터를 사용하기 때문에 한 번에 모든 데이터를 사용하기 어렵습니다. 또 모델이 매우 복잡하기 때문에 수학적인 방법으로 해답을 얻기 어렵습니다.
손실 함수(loss function)
손실 함수는 어떤 문제에서 머신러닝 알고리즘이 얼마나 엉터리인지 측정하는 기준입니다. 그렇다면 손실 함수의 값이 작은것이 좋겠습니다. 하지만 어떤 값이 최솟값인지는 알지 못합니다.
Note: 기술적으로 손실 함수는 미분 가능해야 합니다.(연속적 이다)
종류로는 로지스틱 손실 함수(logistic loss function), 또는 이진 크로스엔트로피 손실 함수(binary cross-entropy loss function) 이 있습니다.
다중 분류에선 손실함수를 크로스엔트로피 손실 함수(cross-entropy loss function)라고 부릅니다.
데이터 준비
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
import pandas as pd
fish = pd.read_csv('https://bit.ly/fish_csv_data')
fish_input = fish[['Weight','Length','Diagonal','Height','Width']].to_numpy()
fish_target = fish['Species'].to_numpy()
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(
fish_input, fish_target, random_state=42)
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
ss.fit(train_input)
train_scaled = ss.transform(train_input)
test_scaled = ss.transform(test_input)
## 모델 학습
from sklearn.linear_model import SGDClassifier
sc = SGDClassifier(loss='log_loss', max_iter=10, random_state=42)
sc.fit(train_scaled, train_target)
print(sc.score(train_scaled, train_target))
print(sc.score(test_scaled, test_target))
---
0.773109243697479
0.775
앞서 이야기한 것처럼 확률적 경사 하강법은 점진적 학습이 가능합니다. SGDClassifier 객체를 다시 만들지 않고 훈련한 모델 sc를 추가로 더 훈련해 봅니다. 모델을 이어서 훈련할 때는 partial_fi() 메소드를 사용합니다. 해당 메소드를 사용할때마다 1에포크씩 이어서 훈련할 수 있습니다.
1
2
3
4
5
6
7
sc.partial_fit(train_scaled, train_target)
print(sc.score(train_scaled, train_target))
print(sc.score(test_scaled, test_target))
---
0.8151260504201681
0.85
아직 점수가 낮지만 에포크를 한 번 더 실행하니 정확도가 향상 됬습니다. 그런데 얼마나 더 훈련해야 할까요? 무작정 많이 반복할 수는 없고 어떤 기준이 필요하겠습니다.
에포크와 과대/과소적합
확률적 경사 하강법을 사용한 모델은 에포크 횟수에 따라 과소적합이나 과대적합이 될 수 있습니다. 에포크 횟수가 적으면 모델이 훈련 세트를 덜 학습합니다. 에포크 횟수가 충분히 많으면 훈련 세트를 완전히 학습할 것 입니다. 훈련 세트에 아주 잘 맞는 모델이 만들어집니다.
적은 에포크 횟수는 훈련 세트와 테스트 세트에 잘 맞지 않는 과소적합, 많은 에포크 횟수는 훈련 세트에 너무 잘 맞아 테스트 세트에서 점수가 나쁜 과대적합 모델일 가능성이 높습니다.
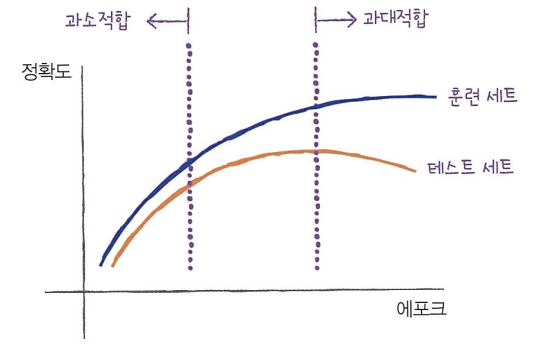
에포크가 진행됨에 따라 훈련 세트 점수는 꾸준히 증가하지만 테스트 세트 점수는 어느 순간 감소하기 시작합니다. 바로 이 지점이 모델이 과대적합되기 시작하는 곳입니다. 과대적합이 시작하기 전에 훈련을 멈추는 것을 조기 종료(early stopping) 라고 합니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import numpy as np
sc = SGDClassifier(loss='log_loss', random_state=42)
train_score = []
test_score = []
classes = np.unique(train_target)
for _ in range(0, 300):
sc.partial_fit(train_scaled, train_target, classes=classes)
train_score.append(sc.score(train_scaled, train_target))
test_score.append(sc.score(test_scaled, test_target))
import matplotlib.pyplot as plt
plt.plot(train_score)
plt.plot(test_score)
plt.xlabel('epoch')
plt.ylabel('accuracy')
plt.show()
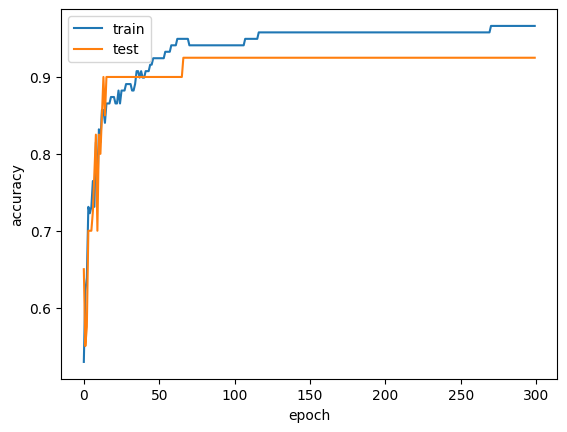
백 번쨰 에포크 이후에는 훈련 세트와 테스트 세트의 점수가 조금씩 벌어지고 있습니다. 또 확실히 에포크 초기에는 과소적합되어 훈련 세트와 테스트 세트의 점수가 낮습니다. 이 모델의 경우 백 번째 에포크가 적절한 반복 횟수로 보입니다.
위의 정보를 바탕으로 결과를 확인 합니다.
sc = SGDClassifier(loss='log_loss', max_iter=100, tol=None, random_state=42)
sc.fit(train_scaled, train_target)
print(sc.score(train_scaled, train_target))
print(sc.score(test_scaled, test_target))
---
0.957983193277311
0.925