Trigonometry for Game Programming – SpriteKit and Swift Tutorial: Part 1/2의 일부분을 의역 했습니다.

Table of contents

Trigonometry for Game Programming – SpriteKit and Swift Tutorial: Part 1/2

SpriteKit, Swift를 사용하는 게임프로그래밍을 위한 삼각법을 배웁니다. 이 이론에 대해서 배우게 되고 그후 space shooter game을 만들며 삼각법을 연습합니다.

Update note: Xcode 9.3, Swift 4.1 iOS 11로 업데이트 되었습니다.

일반적인 오해중 하나는 게임 프로그래머는 수학에 대해서 많이 알아야 한다는 것입니다. 거리와 각도를 계산하는데 수학이 필요하지만 실제로 몇가지 기본 개념을 이해하면 매우 쉽습니다.

이 튜토리얼에서는 삼각함수와, 게임에서 이들을 어떻게 사용하는지에 대해서 배웁니다. 그 후 SpriteKit 프레임 워크를 사용하여 간단한 space shooter iOS 게임을 만들어 보며 이 이론을 적용하고 연습합니다.

지금까지 SpriteKit을 한번도 사용해보지 않았어도, 이 튜토리얼에서 게임을 만들기 위해 다른 프레임 워크 사용하는것을 걱정하지마세요 - 이 튜토리얼에서 다루게되는 수학은 사용할 게임 엔진에 적용 할수 있습니다.

Note: 이 튜토리얼에서 구축할 게임은 가속도계(accelerometer)를 사용합니다. 그래서 iOS 장비와 개발자 계정이 필요합니다.

Getting Started

삼각법(Trigonometry). 한번에 말하기 힘든것 처럼 들릴수 있지만 trigonomety(or 짧게 trig)의 간단하게 삼각형을 계산하는걸 의미합니다.(tri 는 여기서 왔습니다.)

아마 이걸 깨닫지 못했을 것입니다. 하지만 게임들은 삼각형으로 꽉차 있습니다. 예로, 우주선 게임을 상상하고 이 두개의 우주선사이의 거리를 계산하길 원한다고 상상해보세요.


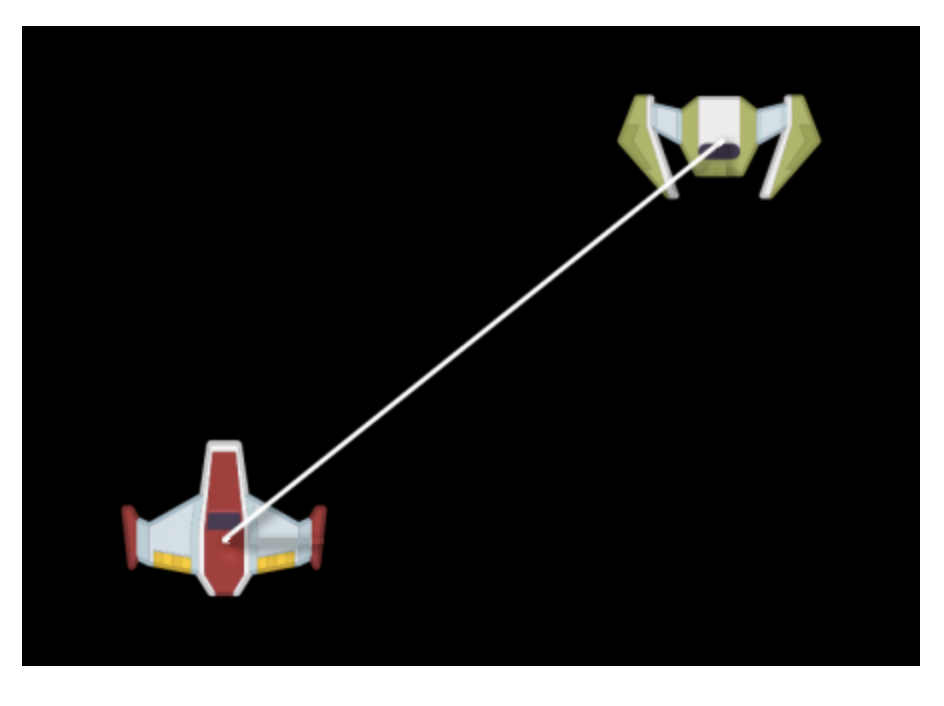
각 우주선의 X,Y 위치를 알지만 흰색의 대각선(diagonal)의 길이를 어떻게. 찾을수 있나요?

음, 다음과같이 삼각형을 각 우주선의 중심점 사이에 간단하게 그릴수 있습니다.


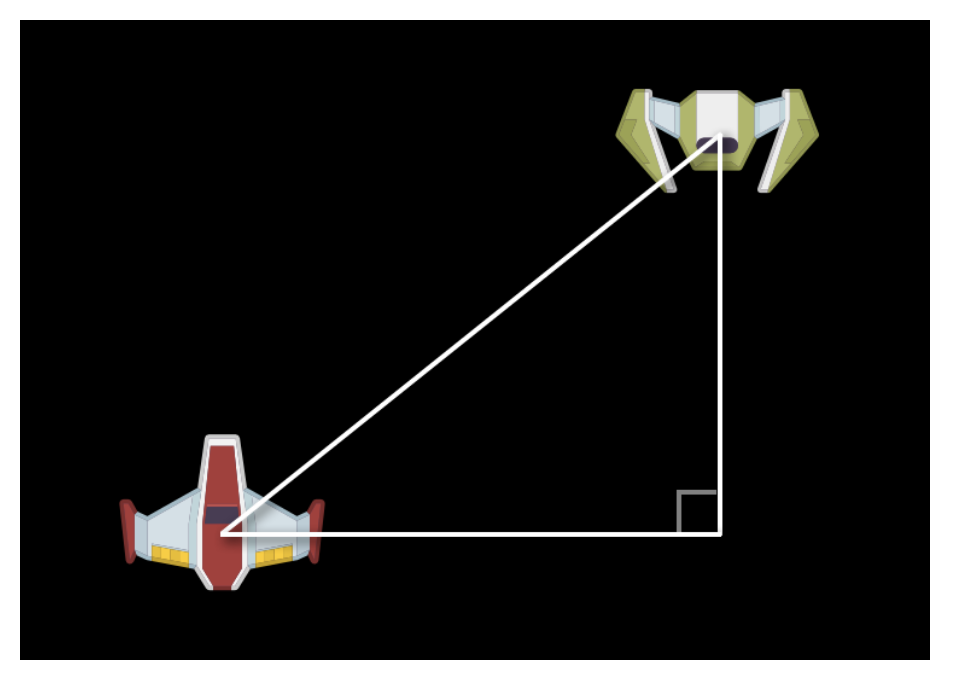
이 삼각형의 모서리중 하나는 90도 입니다. 이 것은 이 튜토리얼에서 다루는 삼각형 타입(triangle)과 직각 삼각형(right triangle)으로 알려져 있습니다.

그림에서 두개의 우주선(sprites)사이의 공간 관계(spatial relationship)와 같이 90도 직각을 가진 삼각형으로 게임에서 무언가 표현할수 있습니다. - 삼각함수를 사용하여 이들을 계산할수 있습니다.

예를들면, 먼저 게임 속에서 다음의 것들이 요구되어질수 있습니다.

  • 우주선은 다른 우주선의 방향으로 레이저를 쏠수 있습니다.
  • 우주선은 다른 우주선을 뒤쫓기 위해 다른 우주선의 방향으로 움직일수 있습니다.
  • 적이 가까워질때 경고 효과를 줄수 있습니다.

삼각법으로 이 모든것과, 그 이상을 할수 있습니다.

Your Arsenal of Functions

먼저, 이론을 알아 봅니다. 걱정마세요 가능한 빠르게 코딩 조각들을 재미있게 읽을수 있도록 짧게 하겠습니다.

이들은 직각 삼각형을 구성하는 부분들입니다.

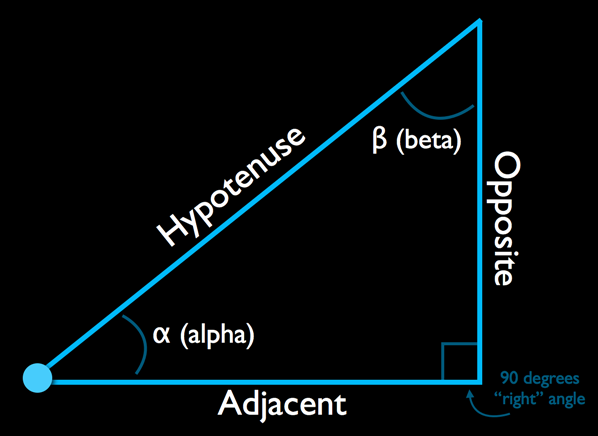
위의 이미지에서, 빗변(diagonal)은 hypotenuse 입니다. 빗변은 항상 직각과 맞은편(across)에 있고 3개의 변중 가장 긴변입니다.

두개의 남아있는 변은 삼각형의 왼쪽 하단 모서리에서 봤을때 adjacent, opposite 라고 합니다.(밑변 또는 높이, 사실 바라보는 기준에 따라서 달라질수 있습니다)

오른쪽 상단 모서리에서 삼각형을 보면 adjacent, opposite 변의 위치가 서로 바뀌게 됩니다.

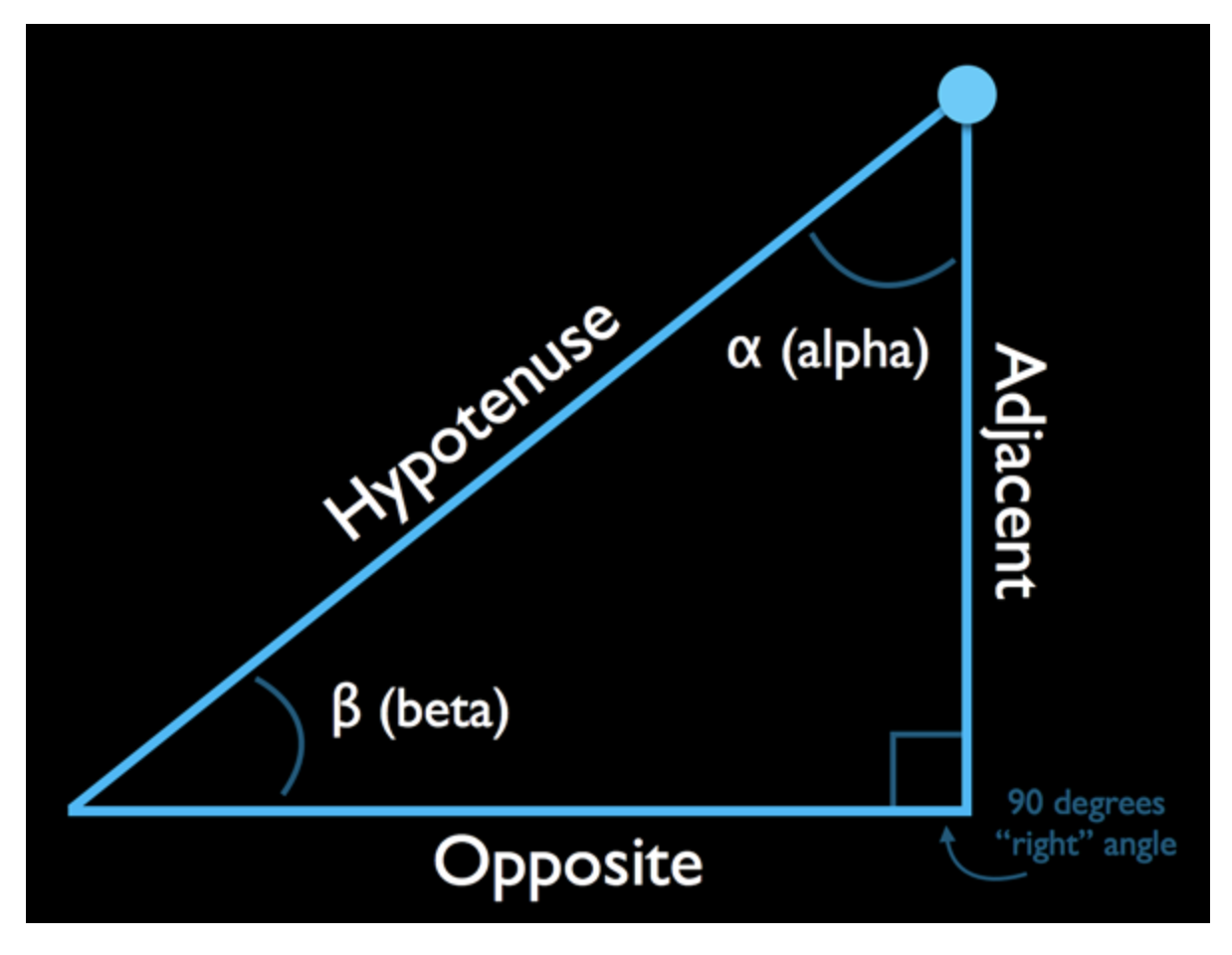
알파(Alpha[α])와 베타(beta[β])는 두개의 다른 각도 이름입니다. 이 각을 원하는대로 부를수 있습니다(그리스 어로 들리는 동안에는). 하지만 일반적으로 알파는 내가 알고싶은 모서리의 각 이고 베타는 반대쪽 모서리의 각도 입니다(usually alpha is the angle in the corner of interest and beta is the angle in the opposing corner). 이 다른 단어들은, 알파에 대해서 반대쪽(opposite), 인접한(adjacent) 변을 식별합니다(label).

멋진점은 두 요소를 모두(변 과 비 직각(non-right angles)) 알고있다면, 삼각법은 삼각함수들(sine, cosine, tangent)를 사용하여 모든 남아있는 변과 각을 찾을수 있게 해줍니다. 예를 들어 각과 변의 하나의 길이를 알고 있다면 다른 변과 모서리의 각과 길이를 쉽게 다룰수 있게 해줍니다.

사인, 코사인, 탄젠트 함수는(짧게는 sin, cos, tan) 단지 비율(just ratios)일 뿐 입니다. 다시 말해 알파와 하나의 변의 길이를 알면 그후 사인, 코사인, 탄젠트는 두 변과 각과 함께 관련된 비율입니다.

사인, 코사인, 탄젠트 함수를 블랙 박스(black boxes)라고 생각하세요 - 숫자를 연결하고 결과를 얻습니다. 이것은 표준 라이브러리 함수로 Swift를 포함한 대부분의 프로그래밍 언어에서 사용할수 있습니다.

Note: 삼각함수의 작용은(The behavior of the trigonometric) 직선으로 원을 투영하여 자세하게 설명되어질수 잇지만, 이를 사용하기 위해 함수를 추론하는(derive) 방법을 알아야할 필요가 없습니다. 궁금하다면, 이걸 자세하게 설명하는 비디오와, 사이트가 있습니다; 이 사이트 Math is Fun을 확인하세요.

Know Angle and Length, Need Sides

예를 들어 보겠습니다. 우주선들 사이의 알파각은 45도 이고, 빗변(hypotenuse)은 10 포인트라고 가정합니다.


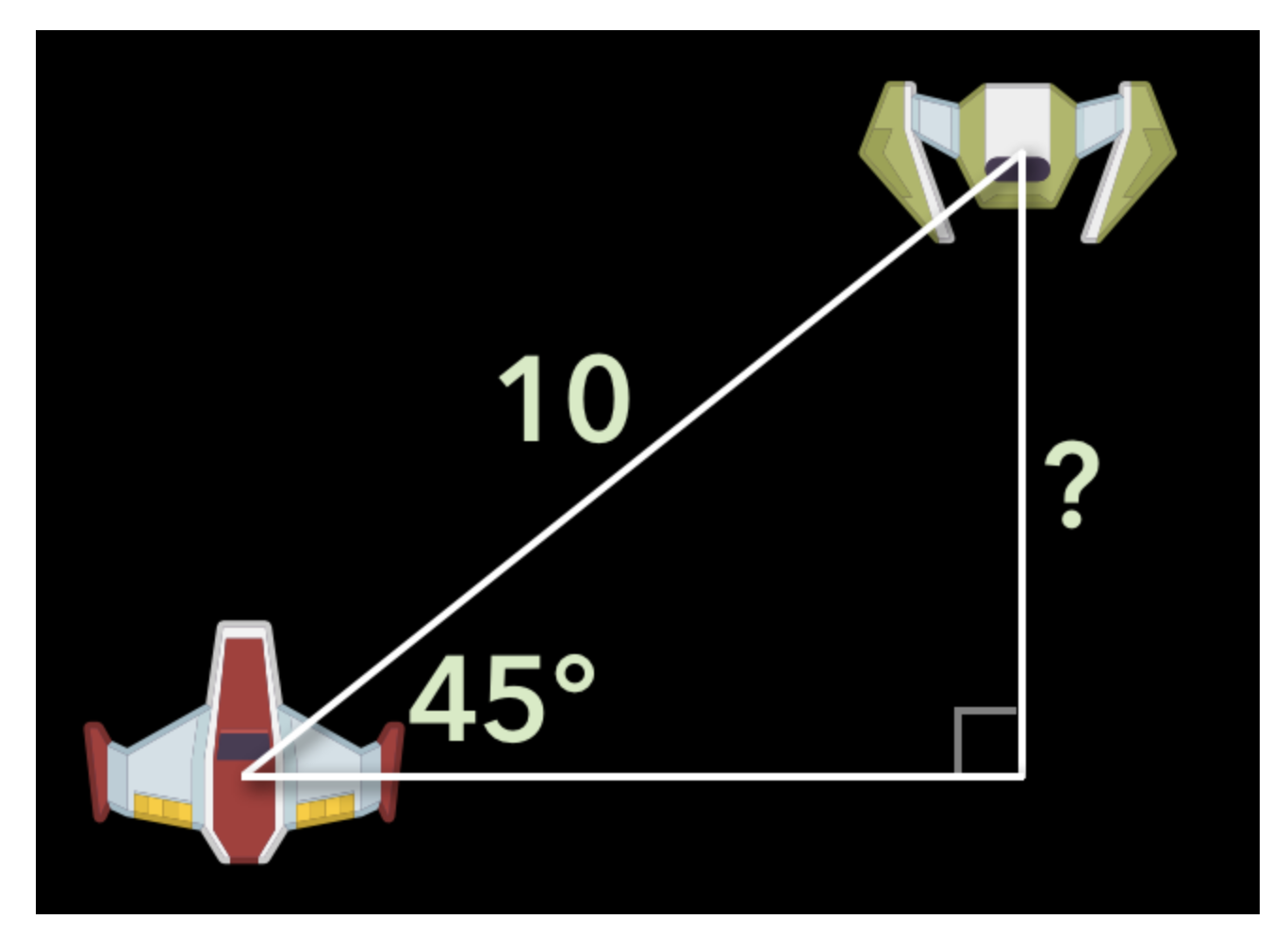
이 값을 다음 공식에 연결할수 있습니다.

sin(45) = opposite / 10

빗변(hypotenuse)에 대한 이것을 해결 하려면 간단하게 이 공식을 다음과같이 이동시킵니다(shift)

opposite = sin(45) * 10

sin(45)는 0.707도 입니다(소수 3자리로 반올림합니다), 주어진 결과를 공식에 채웁니다.

oppsite = 0.707 * 10 = 7.07

Know 2 Sides, Need Angle

위의 공식은 이미 각을 알고 있을때 유용합니다. 하지만 항상 그런것은 아닙니다. 때로는 두 변을 알고 그들 사이의 각을 찾고 있습니다. 각도를 유도하려면 호 함수(arc functions)으로 알려진 역 삼각함수(inverse trig functions)을 사용할수 있습니다.

  • angle = arcsin(opposite / hypotenuse)
  • angle = arccos(adjacent / hypotenuse)
  • angle = arctan(opposite / adjacent)

sin(a) = b 이면, arcsin(b) = a 입니다. 이 역 삼각함수 중에서 arc tangent(arctan)을 대부분 이 연습에서 사용합니다 왜냐하면 이것은 빗변(hypotenuse)를 찾기에 유용합니다. 때로는 이 함수는 sin-1, cos-1, **tan-1(-1</su> 지수의 의미가 아니라는 의미)**로 작성 되므로 혼동하지 마세요.

Know 2 Sides, Need Remaining Side

때로는 두 변의 길이를 알고 나머지 세번째 변을 알아야 합니다. 여기는 피타고라스 이론이 구원해줍니다.

a2 + b2 = c2

또한 삼각형 변의 용어로 사용하면

opposite2 + adjacent2 = hypotenuse2

두 변을 안다면, 공식에서 세번째 변을 아는것은 간단한 제곱근(square root)을 취하는 문제 입니다. 이것은 게임에서 할수 있는 매우 흔한 일이며, 이 튜토리얼에서 여러번 할것입니다.

Note: 공식을 훈련하길 원한다면 Youtube에 Pythagoras song을 검색 해보세요.

Have Angle, Need Other Angle

마지막으로 각도를 고려하세요. 삼각형에서 직각이 아닌 각도 중 하나를 알고 있다면, 다른 것을 아아내는것은 케이크의 조각입니다. 삼각형에서 세 각의 합은 항상 180도 입니다. 왜냐하면 이것은 직각 삼각형 이기 때문입니다(세개의 각중 하나는 90도)

alpha + beta + 90 = 180

또는 간단하게

alpha + beta = 90

남아있는 두각의 합은 90도 입니다. 따라서 알파를 알고있다면 베타를 계산할수 있고 그 반대의 경우에도 가능합니다.

그리고 이것들은 알아야하는 모든 공식입니다. 연습에서 이를 사용하려면 얼만큼 알고 있는가에 달려있습니다. 일반적으로 각, 최소한 하나의 변을 가지고 있거나, 각을 가지진 않았지만 두 변의 길이를 알고있는 경우 입니다.

이제 이론은 충분합니다. 연습을 시작해봅니다.

Begin the Trigonometry!

여기에서 시작 프로젝트를 다운받습니다.

시작 프로젝트는 SpriteKit 프로젝트 입니다. iOS 기기에서 빌드하고 실행하세요. 가속도계가 있는 화면 중앙에 대포와 함께 이동할수 있는 우주선이 있습니다. 두 sprite는 그들 아래에 꽉찬 에너지 바(full health bar)가 있습니다.

현재 우주선은 움직일때 회전하지 않습니다. 우주선이 항상 위로 향하게 하는것보다는 움직이는 것처럼 우주선이 향하고 있는 곳을 바라보는 것이 도움이 될것입니다. 우주선이 회전하려면 회진시킬 각도를 알아야합니다. 하지만 이것이 아직 무엇인지 알지 못합니다 - 벡터 속도계(velocity vector)를 가지고 있습니다 - 그렇다면 벡터로 부터 어떻게 각도를 얻을수 있습니까?

한번 고민해보세요. 플레이어는 X-방향 속도길이와, Y-방향 속도 길이를 가집니다. (The player has the X-direction velocity length and Y-direction velocity length)

이들을 조금 재배치하면 이들이 구성하는 삼각형을 볼수있습니다.

여기서 인접(adjacent(playerVelocity.dx)과 알파 반대편의 변(opposite(playerVelocity.dy))를 알수 있습니다.

그래서 기본적으로, 삼각형의 2개의 변을 알고 각을 찾으려고 합니다(위의 2개의 변을 알고, 각이 필요한경우) 역 삼각함수(arcsin, arccose, arctan) 중에 하나를 사용해야합니다.

알고있는 변은 opposite, adjacent이고 이 변들은 필요한 각의 측면입니다. 따라서 우주선의 회전 각을 찾기 위해 arctan 함수를 사용합니다. 다음과 같은 것을 기억하세요

angle = arctan(opposite / adjacent)

스위프트 표준 라이브러리는 아크 탄젠트를 연산하는 atan()함수가 내장되어 있지만, 몇가지 한계가 있습니다. 먼저, x / y는 -x / -y와 같이 정확히 같은 값은 산출합니다. 반대 속도(opposite velocities)를 위해 같은 각도를 얻을수 있습니다. 둘째로 삼각형 내부의 각은 정확히 원하는 각이 아닙니다 - 하나의 특정 축에 관계된 각(atan()에 반환된 각에서 90, 180, 270도 오프셋이 될수 있습니다)을 얻기를 원합니다.

각도가 어느 사분면인지 결정하기 속도 기호(the velocity signs)를 고려하여 정확한 각도를 적용하기 위해 4방향 if문을 작성할수 있습니다. 그러나 훨씬 간단한 방법이 있습니다.

이 특정 문제에서, atan()을 사용하것 대신, x와 y를 구성 요소를 별도의 매개변수로서 사용하는 atan2(_:_:)함수를 사용하는 것이 더 간단하며 전체 회전 각도를 올바르게 결정합니다.

angle = atan2(opposite, adjacent)

GameScene.swift 에서updatePlayer(_:)의 끝에 다음 코드를 추가합니다.

let angle = atan2(playerVelocity.dy, playerVelocity.dx)
playerSprite.zRotation = angle

Y좌표를 가장 먼저 작성합니다. 첫번째 매개변수는 반대편 변(opposite side)임을 기억하세요. 이 경우에 Y좌표는 측정하려는

앱을 빌드하고 실행합니다.

흠 이것은 잘 동작하지 않는것 같습니다. 이 우주선은 분명히 회전하지만 향해야하는 방향이 아닌 다른 방향을 가리키고 있습니다.

무슨일이 일어났는지: spaceship sprite image 는 똑바로 올라가며 이는 0도의 기본 회전값에 해당합니다. 하지만 수학적으로 0도는 위쪽을 향하지만 오른쪽의 X축은 다음과 같습니다.

이것을 고치려면 회전 각도에서 90도를 빼야합니다.

playerSprite.zRotation = angle - 90

앱을 다시 빌드하고 실행해봅니다.

Radians, Degrees and Points of Reference

일반적인 사람은 각도를 0~360도 사이의 값으로 생각하는 경향이 있습니다. 수학자들은 일반적으로 라디안(radians)으로 각도를 측정하는데 π(그리스 문자 Pi, pie처럼 들립니다)로 표시합니다.

1라디안은 호를 따라 이동한 반지름의 길이만큼 이동할때 얻는 각도 입니다. 원의 시작 부분에서 끝까지 2π 주기(대략 6.28번) 입니다.


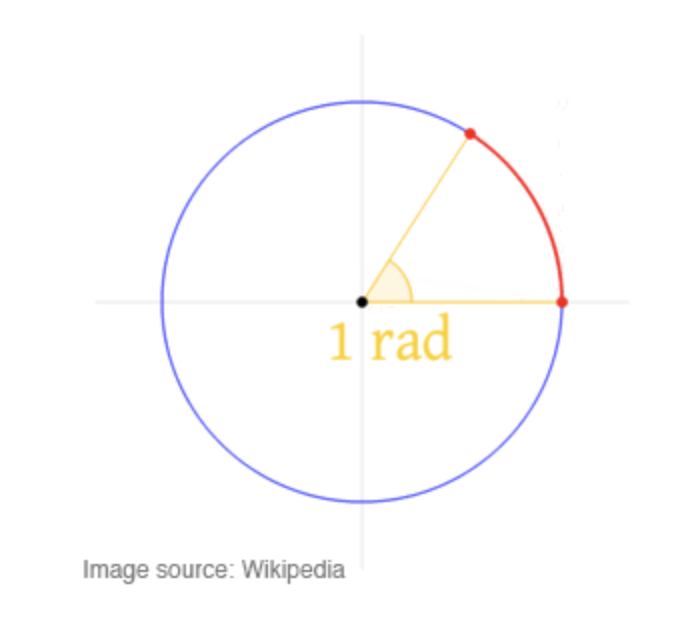
반지름(노란색 선)은 호(빨간색 곡선)같은 길이를 가집니다. 두 길이가 같은 각도는 1라디안 입니다.

0에서 360도 까지의 각도로 표현할수 있지만, 또한 0-2π까지 표현할수도 있습니다. 대부분의 컴퓨터에서는 수학 함수는 라디안 단위로 작동합니다. SpriteKit은 모든 각도 측정에 라디안을 사용합니다. atan2(_:_:) 함수는 라디안 단위로 값을 반환하지만, 각도를 90도로 조정(offset)하려고 했습니다.

라디안과 각도 모두 함께 사용하기 때문에, 둘사이를 쉽게 변환할수 있는 방법이 유용합니다. 변환은 매우 간단합니다. 원 안에 2π 또는 360도 가 있기 때문에 π는 180도 입니다. 라디안을 도(degrees)로 변환하려면 180 / π를 곱해주면 됩니다. 각도를 라디안으로 변환하려면 π / 180을 곱해줍니다.

GameScene위의 두개의 제약조건을 추가합니다.

let degreesToRadians = CGFloat.pi / 180
let radiansToDegrees = 180 / CGFloat.pi

마지막으로, updatePlayer(_:)에 있는 회전 코드를 degreesToRadians을 사용하여 편집합니다.

playerSprite.zRotation = angle - 90 * degreesToRadians

다시 빌드하고 실행합니다. 마침내 우주선이 회전하고 머리 방향으로 방향합니다.

Bouncing Off the Walls

가속도계를 사용하여 이동하는 우주선이 있습니다. 삼각함수를 사용하여 방향으로 향하게 만들어야합니다.

우주선이 화면의 가장 자리에 달라붙는 것은 그리 만족스럽지 않습니다. 스크린 테두리에서 우주선을 튀어 오르게 하여 이것을 고칩니다.

먼저 updatePlayer(_:)에서 다음 행을 삭제합니다.

newX = min(size.width, max(0, newX))
newY = min(size.height, max(0, newY))

그후 다음의 것들로 교체합니다.

var collidedWithVerticalBorder = false
var collidedWithHorizontalBorder = false

if newX < 0 {
  newX = 0
  collidedWithVerticalBorder = true
} else if newX > size.width {
  newX = size.width
  collidedWithVerticalBorder = true
}

if newY < 0 {
  newY = 0
  collidedWithHorizontalBorder = true
} else if newY > size.height {
  newY = size.height
  collidedWithHorizontalBorder = true
}

이것은 우주선이 화면의 끝부분에 부딛혔는지 검사하고, 부딛혔다면 Bool 값을 true로 변경합니다. 우주선이 경계에서 튀어 오르게 하려면 속도(velocity)와 가속도(acceleration)를 뒤바꿉니다.

방금 추가한 코드 바로 아래에 다음 코드를 추가합니다.

if collidedWithVerticalBorder {
  playerAcceleration.dx = -playerAcceleration.dx
  playerVelocity.dx = -playerVelocity.dx
  playerAcceleration.dy = playerAcceleration.dy
  playerVelocity.dy = playerVelocity.dy
}

if collidedWithHorizontalBorder {
  playerAcceleration.dx = playerAcceleration.dx
  playerVelocity.dx = playerVelocity.dx
  playerAcceleration.dy = -playerAcceleration.dy
  playerVelocity.dy = -playerVelocity.dy
}

충돌이 등록되면, 가속도와 속도값이 반전되고 우주선이 다시 튀어 오릅니다.

앱을 빌드하고 실행합니다.

바운싱이 작동하지만 너무 과하게 동작하는것 같습니다. 이 문제는 우주선이 탱탱볼 처럼 튀어오르는것을 기대하지 않았다는 것입니다. 충돌시 에너지를 대부분 잃어 버리고, 이전보다 작은 속도로 이탈합니다.

maxPlayerSpeed: CGFloat = 200 아래에 다음 상수를 추가하세요

let bordercollisionDamping: CGFloat = 0.4

이제 updatePlayer(_:)에 추가된 코드를 다음과같이 변경합니다.

if collidedWithVerticalBorder {
  playerAcceleration.dx = -playerAcceleration.dx * bordercollisionDamping
  playerVelocity.dx = -playerVelocity.dx * bordercollisionDamping
  playerAcceleration.dy = playerAcceleration.dy * bordercollisionDamping
  playerVelocity.dy = playerVelocity.dy * bordercollisionDamping
}

if collidedWithHorizontalBorder {
  playerAcceleration.dx = playerAcceleration.dx * bordercollisionDamping
  playerVelocity.dx = playerVelocity.dx * bordercollisionDamping
  playerAcceleration.dy = -playerAcceleration.dy * bordercollisionDamping
  playerVelocity.dy = -playerVelocity.dy * bordercollisionDamping
}

가속도와 속도에 제동값(damping value = bordercollisionDamping)를 곱해주면 됩니다. 충돌을 통해 잃어 버리는 많은 에너지를 어떻게 통제하는지 알수 있게 해줍니다. 이 경우 화면의 가장자리로 충돌 부딪힌 이후에 우주선의 속도의 40%만 유지하도록 만듭니다.

재미를 위해서 bordercollisionDamping의 값을 다른 값으로 변경하여 확인해보시길 바랍니다. 이 값을 1.0보다 크게 한다면, 실제로 우주선은 충돌로 에너지를 얻습니다.

약간의 문제가 있음을 눈치 챘을것 입니다: 우주선을 계속해서 화면 아래쪽으로 두면 화면의 경계를 계속 부딛히면서 위, 아래를 오가며 마침내 방향을 모호하게 가리키는 걸 확인할수 있습니다.

X와 Y가 꾀 큰값이라면 아크 탄젠트를 사용하여 X와 Y 구성요소 사이의 각도를 찾습니다. 이 경우에 제동 펙터는 대부분 값을 0으로 줄입니다. atan2(_:_:)를 매우 작은 값으로 적용하면 이 값을 약간만 변경해도 결과 각도가 크게 변될수 있습니다.

이 문제를 해결하는 한가지 방법은 속도가 느릴때 각도를 변경하지 않는 것입니다. 이것은 피타고라스를 사용할 좋은 기회입니다.

사실 우주선의 속도(ship's speed)를 저장하지 않았습니다. 대신 벡터와 동일한 속도(speed와 velocity 사이의 차이에 대한 설명은 여기를 참조해주세요 )인 velocity를 X-방향 과 Y방향에 있는 구성요소와 함께 저장합니다. 하지만 우주선의 속도(ship’s speed)를 결정하기 위해(우주선을 돌릴 가치가 있는 속도가 너무 느린지 등) 이 X와 Y 속도 구성요소를 단일 스칼라 값으로 결합해야합니다.

Personal Note:
velocity = scalar + vector (속도 + 방향)
speed = scalar (속도만)
속도와 속력의 차이

여기서는 앞에서 논의 했던 2개의 변을 알고있을때 남은 변을 아는 방법을 사용압니다.

보다시피, 우주선의 실제 속도는 - 초당 스크린에서 얼마나많은 지점이 움직이 움직이는지 - X 와 Y 방향의 속도에 의해서 생성된 삼각형의 빗변입니다.

피타고라스 공식의 용어로 표현하면:

true speed = √(playerVelocity.dx2 + playerVelocity.dy2)

updatePlayer(_:)에서 다음 블록을 지웁니다.

let angle = atan2(playerVelocity.dy, playerVelocity.dx)
playerSprite.zRotation = angle - 90 * degreesToRadians

그리고 다음으로 대체합니다.

let rotationThreshold: CGFloat = 40

let speed = sqrt(playerVelocity.dx * playerVelocity.dx + playerVelocity.dy * playerVelocity.dy)
if speed > rotationThreshold {
  let angle = atan2(playerVelocity.dy, playerVelocity.dx)
  playerSprite.zRotation = angle - 90 * degreesToRadians
}

빌드하고 실행합니다. 화면의 가장 자리에서 좀더 안정적으로 회전하는 우주선을 볼수 있습니다. 40의 값의 용도가 무엇인지 궁금하다면 답은 실험입니다. 코드에 print()를 사용하여 화면의 경계에 부딪혔을대 속도를 살펴보면 올바른 값이 라고 생각할때까지 조정하는데 도움이됩니다.

Blending Angles for Smooth Rotation

물론 어떤 하나의 각을 고정하면 어떤것들을 깨뜨릴수 있습니다. 우주선이 멈출때까지 우주선을 감속시킨후, 다음으로 우주선이 돌아서서 다른 방향으로 날아갈수 있도록 장치를 뒤집어보세요.

이전에는 우주선이 실제로 선회하는 멋진 애니메이션을 볼수 있었습니다. 그러나 우주선이 저속에서 각도를 변경하지 못하도록하는 코드를 추가했으므로 이제 선회가 매우 갑작스럽(sbrupt) 습니다. 작은 디테일 이지만 멋진 앱과 게임을 만드는것은 이러한 디테일 입니다.

이 위치 결정은 즉각적으로 새 각도로 전환하지 않고 연속된 프레임에 대해서 이전각도와 서서히 조합되어 변경된다는(blend) 것입니다. 우주선이 충분히 빠르게 움직이지 않을때 회전하는 동안 선회 애니메이션을 다시 도입합니다.

이 블렌딩(blending)은 멋지게 들리지만 사실 구현하기 쉽습니다. 업데이트 사이의 우주선의 각도를 기록하는게 필요합니다. GameScene 클레스에 다음 속성을 추가합니다.

var playerAngle: CGFloat = 0

rotationThreshold의 선언에서 updatePlayer(_:)의 if 조건문 끝에 있는 코드를 다음 코드로 교체합니다.

let rotationThreshold: CGFloat = 40
let rotationBlendFactor: CGFloat = 0.2

let speed = sqrt(playerVelocity.dx * playerVelocity.dx + playerVelocity.dy * playerVelocity.dy)
if speed > rotationThreshold {
  let angle = atan2(playerVelocity.dy, playerVelocity.dx)
  playerAngle = angle * rotationBlendFactor + playerAngle * (1 - rotationBlendFactor)
  playerSprite.zRotation = playerAngle - 90 * degreesToRadians
}

playerAngle은 새로운 각도와 이전 각도에 블렌드 펙터(blend factor)을 곱셈하여 결합합니다. 즉, 새로운 각은 우주선에 설정한 실제 회전 방향에 20% 밖에 기여하지 않았습니다. 시간이 지남에 따라 더 많은 새로운 각도가 추가되고 결국 우주선이 향하고 있는 방향을 가리킵니다.

하나의 회전 각도에서 다른 회전각도로 극적인 변화가 더 이상 없음을 확인하기 위해 빌드하고 실행합니다.


이제 시계방향과 시계 반대 방향 둘다 원을 그리며 비행 해보세요. 어느 지점에서 우주선은 갑자기 반대방향으로 360도 회전합니다. 이것은 원의 동일한 지점에서 항상 발생합니다. 무슨일인가요?

atan2(_:_:)는 +π, -π(180도 와 -180도)사이의 각도를 반환합니다. 이것은 현재 각도가 +π와 매우 가깝고 이때 조금더 회전하면 -π로(또는 그 반대) 뒤집는걸 의미합니다.

실제로 원에서 같은 위치에 해당합니다(-180도 와 +180도느 같은 위치) 하지만. 블렌딩(blending) 알고리즘은 이것을 알아 차릴만큼 충분히 똑똑하지 않습니다. - 각도는 첫번째 단계에서 전체 360도를 뛰어넘고, 반대방향으로 360도 회전시켜 되돌려야합니다.

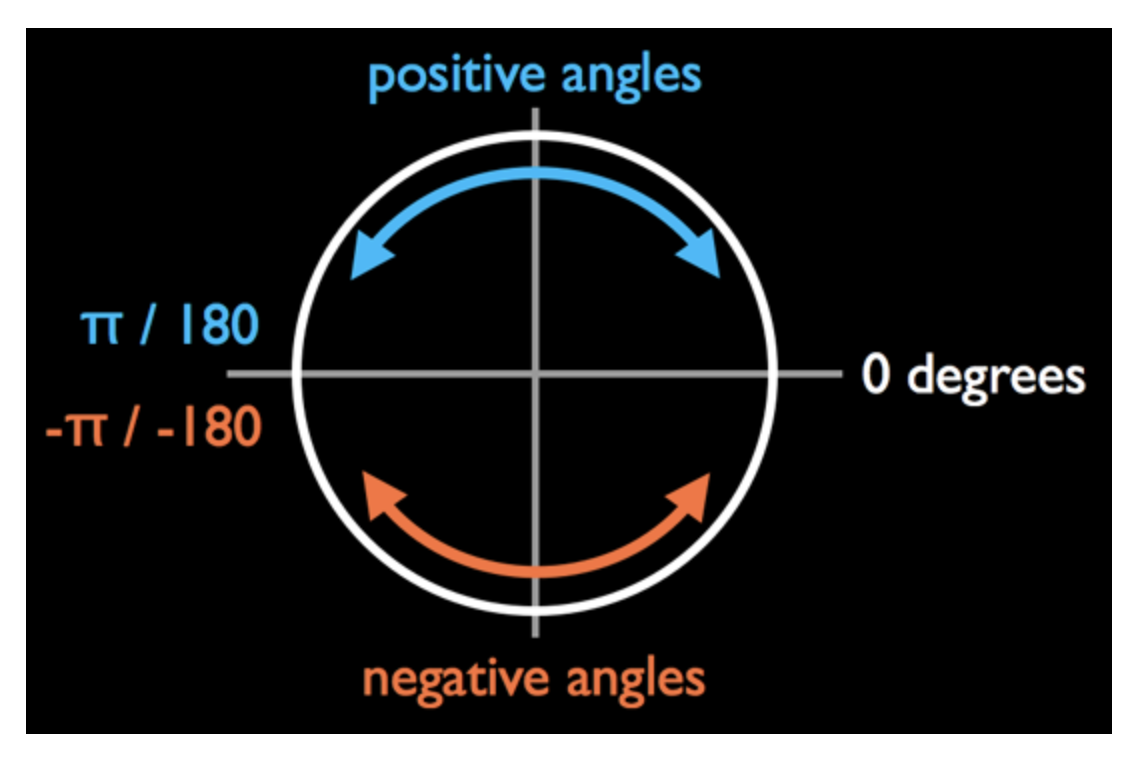
이를 수정하려면 각도가 임계 값(threshold)을 초과할때를 인식하고 이에 따라 playerAngle을 조정해야합니다. GameScene 클레스에 새 속성을 추가합니다.

var previousAngle: CGFloat = 0

다시, rotationThreshold 선언에서 updatePlayer(_:) 조건 끝가지 작성된 코드를 다음 코드로 변경합니다.

let rotationThreshold: CGFloat = 40
let rotationBlendFactor: CGFloat = 0.2

let speed = sqrt(playerVelocity.dx * playerVelocity.dx + playerVelocity.dy * playerVelocity.dy)
if speed > rotationThreshold {
  let angle = atan2(playerVelocity.dy, playerVelocity.dx)
  
  // did angle flip from +π to -π, or -π to +π?
  if angle - previousAngle > CGFloat.pi {
    playerAngle += 2 * CGFloat.pi
  } else if previousAngle - angle > CGFloat.pi {
    playerAngle -= 2 * CGFloat.pi
  }
  
  previousAngle = angle
  playerAngle = angle * rotationBlendFactor + playerAngle * (1 - rotationBlendFactor)
  playerSprite.zRotation = playerAngle - 90 * degreesToRadians
}

이제 현재 각도와 이전 각도 사이의 차이를 확인하고 임계값(0-π(180도)) 이상을 확인하고 이것을 고쳐야합니다.

앱을 빌드하고 실행합니다. 이전과 동일한 문제가 없어야합니다.