Code
func example(str: String, isAction: Bool = true, action: () -> Void) {
print("---------\(str), isAction: \(isAction)---------")
if isAction {
action()
}
}
func createRandomArray(numberOfElements: Int = 10) -> [Int] {
var randomIntInArray: [Int] = [Int]()
while randomIntInArray.count != numberOfElements {
let popRandomValue = Int(arc4random_uniform(11))
randomIntInArray.append(popRandomValue)
}
return randomIntInArray
}
example(str: "Merge Sort", isAction: true) {
func mergeSort<T: Comparable>(data: [T]) -> [T] {
print(data)
guard data.count > 1 else { return data }
let middle = data.count / 2
let left = mergeSort(data:Array(data[..<middle]))
let right = mergeSort(data:Array(data[middle...]))
print("middle: \(middle), left:\(left), right:\(right)")
return merge(left, right)
}
func merge<T: Comparable>(_ left: [T], _ right: [T]) -> [T] {
// 1
var leftIndex = 0
var rightIndex = 0
// 2
var result: [T] = []
// 3
while left.count > leftIndex && right.count > rightIndex {
let leftElement = left[leftIndex]
let rightElement = right[rightIndex]
print("leftcount,leftIndex: \(left.count):\(leftIndex), rightcount,rightIndex: \(right.count):\(rightIndex), left,leftElement: \(left):\(leftElement), right,rightElement: \(right):\(rightElement) Result\(result)")
// 4
if leftElement < rightElement {
result.append(leftElement)
leftIndex += 1
print("leftcount,leftIndex: \(left.count):\(leftIndex), rightcount,rightIndex: \(right.count):\(rightIndex), left,leftElement: \(left):\(leftElement), right,rightElement: \(right):\(rightElement) Result\(result)")
} else if leftElement > rightElement {
result.append(rightElement)
rightIndex += 1
print("leftcount,leftIndex: \(left.count):\(leftIndex), rightcount,rightIndex: \(right.count):\(rightIndex), left,leftElement: \(left):\(leftElement), right,rightElement: \(right):\(rightElement) Result\(result)")
} else {
result.append(leftElement)
leftIndex += 1
result.append(rightElement)
rightIndex += 1
print("leftcount,leftIndex: \(left.count):\(leftIndex), rightcount,rightIndex: \(right.count):\(rightIndex), left,leftElement: \(left):\(leftElement), right,rightElement: \(right):\(rightElement) Result\(result)")
}
}
// 5
if leftIndex < left.count {
result.append(contentsOf: left[leftIndex...])
print("leftcount,leftIndex: \(left.count):\(leftIndex), rightcount,rightIndex: \(right.count):\(rightIndex), Result\(result)")
}
if rightIndex < right.count {
result.append(contentsOf: right[rightIndex...])
print("leftcount,leftIndex: \(left.count):\(leftIndex), rightcount,rightIndex: \(right.count):\(rightIndex), Result\(result)")
}
return result
}
let x = createRandomArray(numberOfElements: 10)
print(mergeSort(data:x))
}
배열을 왼쪽 상자 / 오른쪽 상자의 각 값의 크기 비교
- 오른쪽 값이 왼쪽 값보다 크다면 -> result에 왼쪽 값 넣고, LeftIndex +1
- 왼쪽 값이 오른쪽 값보다 크다면 -> result에 오른쪽 값을 넣고, rightIndex +1
- 두 값이 크거나 작지 않으면 -> 두 값을 result에 넣고, 각 인덱스 +1
- 예시 [3,4,8,5,2,1]
- [3,4,8] / [5,2,1] -> 전체를 반으로 나누고 왼쪽, 오른쪽 각각 재귀 하며 조건에 맞는 값에 수렴해감
- [3], [4, 8] -> [3]은 left 확정
- [4, 8] -> merge 호출 각각 4, 8 크기 비교후, 정렬하고 -> [4,8] 반환 -> right 확정
- left: [3], right: [4,8] -> merge 호출
- left의 첫번째 인덱스의 값과, right의 첫번째 인덱스의 값 비교. 오른쪽 값이 큼 result에 3추가, left Index +1 -> while 탈출
- result에 right의 나머지 값을 모두 넣음 result [3,4,8]
- [5], [2, 1] -> left [5]: 확정, right [2, 1]
- [2, 1] -> left [2], right [1] -> merge 호출
- 두 값을 비교후 -> 정렬 -> 반환 [1, 2]
- left [5], right [1, 2] -> merge 호출
- 각 값 비교후 -> 정렬 -> 반환 -> [1, 2, 5]
- left [3,4,8] right [1,2,5] -> merge 호출
- 각 값 비교후 -> 정렬 -> 반환
- result [1, 2, 3, 4, 5, 8]
- 예시 [3,4,8,5,2,1]
Time Complexity
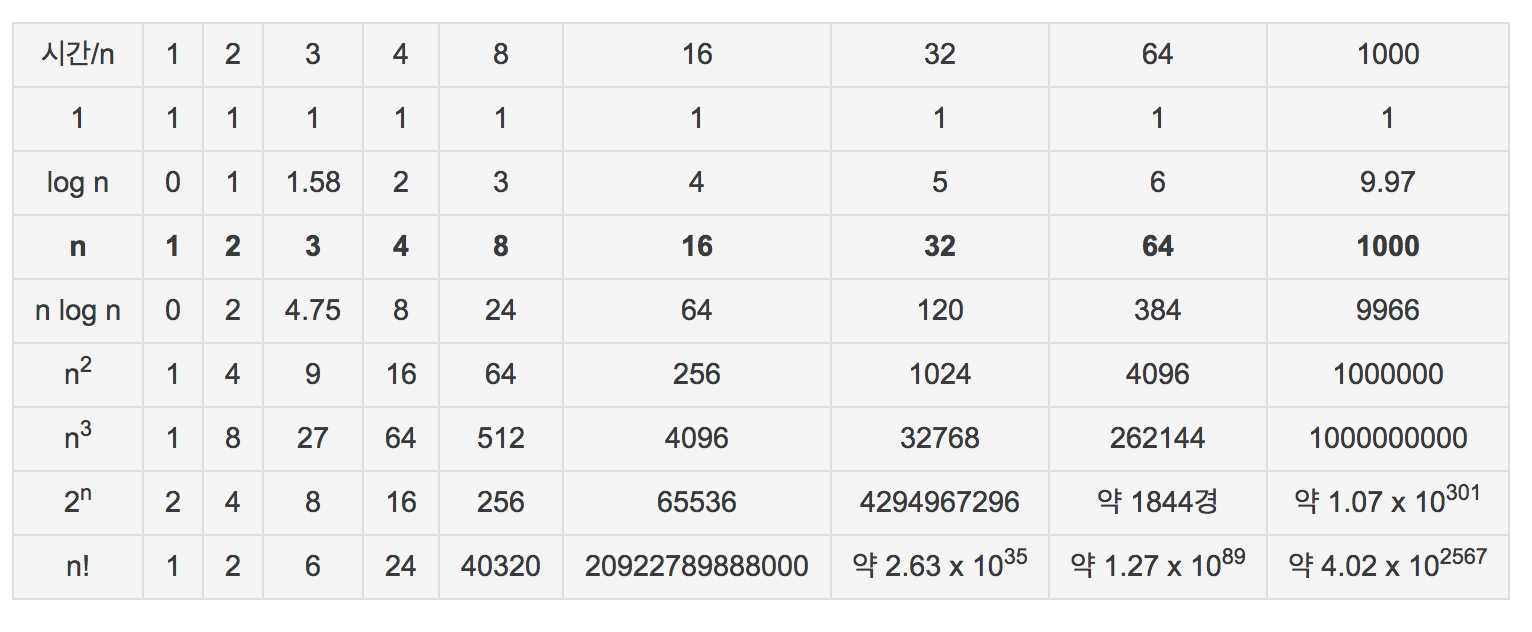
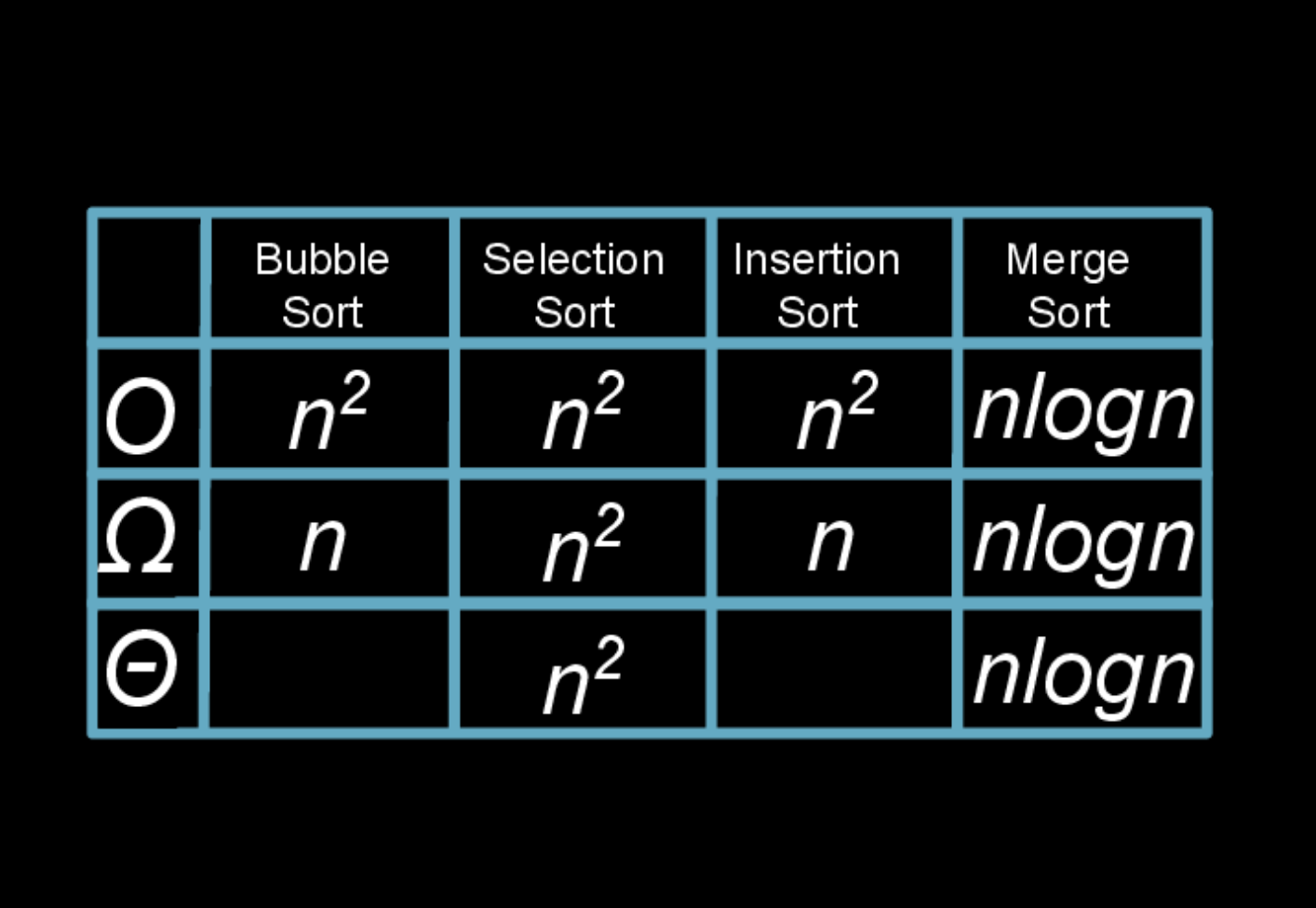
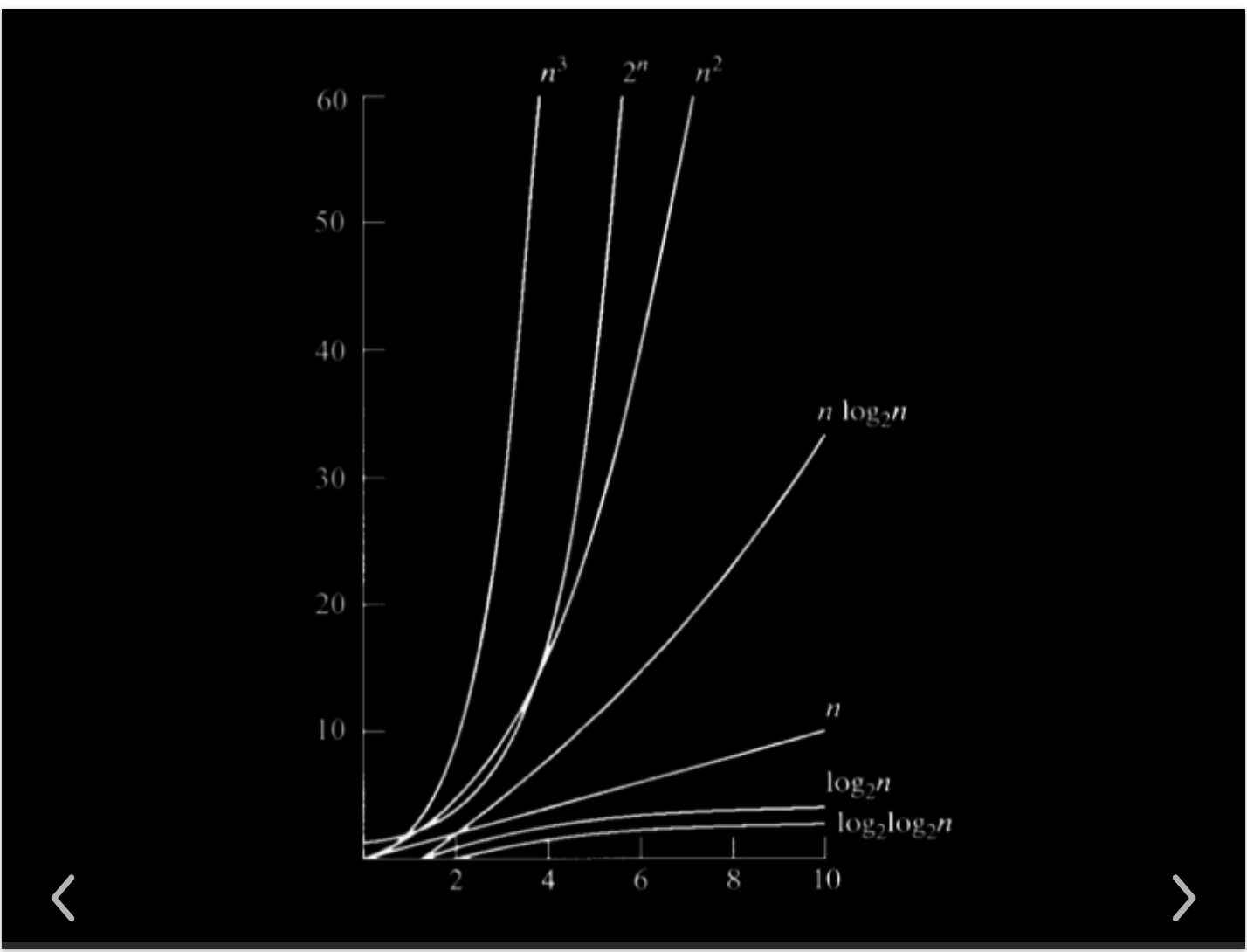
Reference
http://cdn.cs50.net/2014/fall/lectures/4/m/notes4m/notes4m.html#merge_sort
swift-algorithm-club